
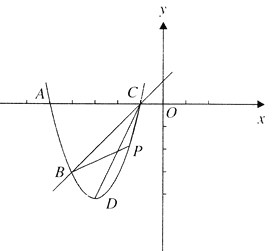
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为顶点,
为顶点,![]() 为抛物线上一动点(与点
为抛物线上一动点(与点![]() 不重合)
不重合)
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
![]() 该抛物线上是否存在点
该抛物线上是否存在点![]() ,使
,使![]() ?若存在,求出所有点
?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)将点A、B、C坐标代入二次函数表达式,即可求解;
(2)利用S△PBC=![]() PG(xCxB),即可求解;
PG(xCxB),即可求解;
(3)分点P在直线BC下方、上方两种情况,分别求解即可.
解:![]() 抛物线过
抛物线过![]() 两点
两点
可设为![]()
又过点![]()
![]()
![]()
![]() 解析式为
解析式为![]() ;
;
![]() ,
,![]()
设直线BC的解析式为y=kx+b
把B,C坐标代入得![]()
解得![]()
![]() 可得直线
可得直线![]() 的解析式为:
的解析式为:![]()
过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]()
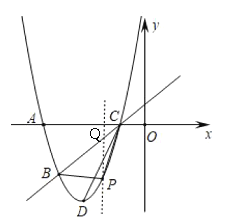
设点![]() 的横坐标为
的横坐标为![]()
则点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]()
![]()
![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() ;
;
![]() 存在.
存在.
∵![]() =
=![]()
∴顶点![]() 的坐标为
的坐标为![]() ,
,
连接![]()
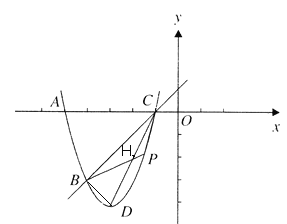
则![]()
![]()
![]() 是直角三角形,且
是直角三角形,且![]() .
.
![]() 当点
当点![]() 在直线
在直线![]() 下方时,
下方时,
设![]() 的中点为
的中点为![]()
则![]() ,
,
且点![]() 为直线
为直线![]() 与抛物线的交点(不与点
与抛物线的交点(不与点![]() 重合)
重合)
设直线![]() 的表达式为y=px+q
的表达式为y=px+q
把B,H的坐标代入得![]()
解得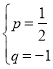
∴直线![]() 的表达式为
的表达式为![]()
令![]() ,
,
解得![]() (舍去)或
(舍去)或![]()
![]() 此时
此时![]() 的坐标为
的坐标为![]()
![]() 当点
当点![]() 在直线
在直线![]() 上方时,
上方时,![]() .
.
设直线CD的解析式为y=mx+n
把C,D的坐标代入得![]()
解得![]()
∴直线![]() 的表达式为
的表达式为![]() ,
,
则可设直线![]() 的表达式为
的表达式为![]()
将点![]() 代入
代入![]() 解得
解得![]()
故直线![]() 的表达式为
的表达式为![]() .
.
令![]() ,
,
解得![]() 或
或![]()
![]() 此时点
此时点![]() 的坐标为
的坐标为![]()
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
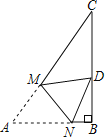
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人依次测量同一圆柱体工件的横截面直径(单位:![]() ),测得的数据分别如表1、表2.
),测得的数据分别如表1、表2.
表1:甲的测量数据
测量数据 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
频数 | 1 | 3 | 3 | 2 | 1 |
表2:乙的测量数据
测量数据 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
频数 | 1 | 2 | 3 | 2 | 2 |
(1)如果在这些测量数据中选择一个数据作为工件直径的估计值,应该是那个数据?请说明理由.
(2)如果甲再测量一次,求他测量出的数据恰好是估计值的概率;
(3)请直接判断甲乙两人谁的测量技术更好______(填甲或乙),你选择的统计量是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方法提炼)
解答几何问题常常需要添辅助线,其中平移图形是重要的添辅助线策略.
(问题情境)
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
小明在分析解题思路时想到了两种平移法:
方法1:平移线段FG使点F与点B重合,构造全等三角形;
方法2:平移线段BC使点B与点F重合,构造全等三角形;
(尝试应用)
(1)请按照小明的思路,选择其中一种方法进行证明;
(2)如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
(3)如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连结DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连结AC交DE于点H,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
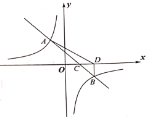
【题目】一次函数![]() 的图像与双曲线
的图像与双曲线![]()
![]() 相交于
相交于![]() 和
和![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求一次函数的解析式;
(2)根据图像直接写出不等式![]() 的解集;
的解集;
(3)![]() 的面积为
的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生参加公益活动,根据该校九年级六个班的同学某星期参加公益活动总人次所绘制了的折线统计图(如图所示),则下列说法正确的是( )
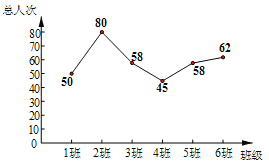
A.极差是40B.平均数是60C.众数是58D.中位数是51.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
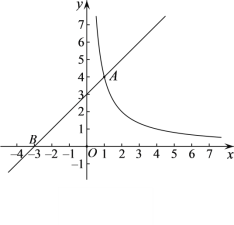
【题目】如图,直线![]() 与函数
与函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)过动点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com