
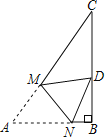
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
【答案】2或3![]() ﹣3
﹣3
【解析】
依据△DCM为直角三角形,需要分两种情况进行讨论:当∠CDM=90°时,△CDM是直角三角形;当∠CMD=90°时,△CDM是直角三角形,分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到AM的长.
解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
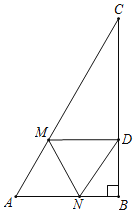
∵在Rt△ABC中,∠B=90°,∠A=60°,AB=3,
∴AC=2AB=6,∠C=30°,由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=![]() DN=
DN=![]() AN,
AN,
∴BN=![]() AB=1,
AB=1,
∴AN=2BN=2,
∵∠DNB=60°,
∴∠ANM=∠DNM=60°,
∴∠AMN=60°,
∴AM=AN=2;
②如图,当∠CMD=90°时,△CDM是直角三角形,
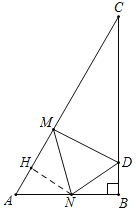
由题可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=![]() DN=
DN=![]() AN,BN=
AN,BN=![]() BD,
BD,
又∵AB=3,
∴AN=6(2﹣![]() ),BN=6
),BN=6![]() ﹣9,
﹣9,
过N作NH⊥AM于H,则∠ANH=30°,
∴AH=![]() AN=3(2﹣
AN=3(2﹣![]() ),HN=6
),HN=6![]() ﹣9,
﹣9,
由折叠可得,∠AMN=∠DMN=45°,
∴△MNH是等腰直角三角形,
∴HM=HN=6![]() ﹣9,
﹣9,
∴AM=AH+HM=3(2﹣![]() )+6
)+6![]() ﹣9=3
﹣9=3![]() ﹣3,
﹣3,
故答案为:2或3![]() ﹣3.
﹣3.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
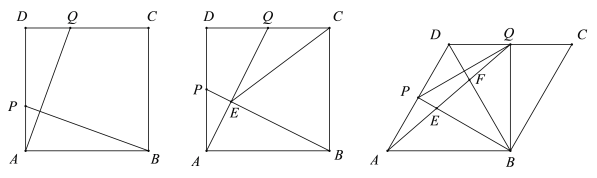
【题目】如图1,边长为6的正方形ABCD,动点P、Q各从点A,D同时出发,分别沿边AD,DC方向运动,且速度均为每秒1个单位长度.
(1)AQ与BP关系为________________;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,试探究∠CEQ和∠BCE满足怎样的数量关系;
(3)如图3,将正方形变为菱形且∠BAD=60°,其余条件不变,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点A的坐标为
中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,抛物线
,抛物线![]() 的顶点为C.
的顶点为C.
(1)若抛物线经过点B时,求顶点C的坐标;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求a的取值范围;
恰有一个公共点,结合函数图象,求a的取值范围;
(3)若满足不等式![]() 的x的最大值为3,直接写出实数a的值.
的x的最大值为3,直接写出实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小腾的爸爸计划将一笔资金用于不超过10天的短期投资,针对这笔资金,银行专属客户经理提供了三种投资方案,这三种方案的回报如下:
方案一:每一天回报30元;
方案二:第一天回报8元,以后每一天比前一天多回报8元;
方案三:第一天回报0.5元,以后每一天的回报是前一天的2倍.
下面是小腾帮助爸爸选择方案的探究过程,请补充完整:
(1)确定不同天数所得回报金额(不足一天按一天计算),如下表:
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中![]() ________;
________;
(2)计算累计回报金额,设投资天数为![]() (单位:天),所得累计回报金额是
(单位:天),所得累计回报金额是![]() (单位:元),于是得到三种方案的累计回报金额
(单位:元),于是得到三种方案的累计回报金额![]() ,
,![]() ,
,![]() 与投资天数
与投资天数![]() 的几组对应值:
的几组对应值:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中![]() ________;
________;
(3)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,
,![]() ,并画出
,并画出![]() ,
,![]() ,
,![]() 的图象;
的图象;
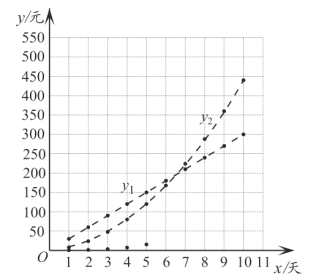
注:为了便于分析,用虚线连接离散的点.
(4)结合图象,小腾给出了依据不同的天数而选择对应方案的建议:
_________________________________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.深圳市环境卫生局为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
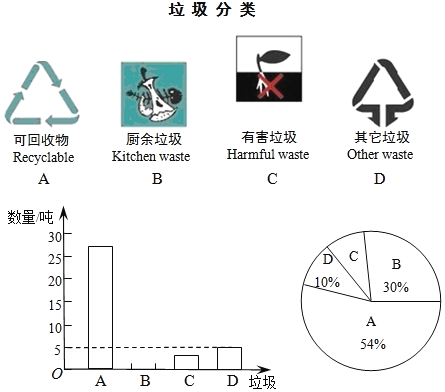
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,产生的有害垃圾C所对应的圆心角为 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设深圳市每天产生的生活垃圾为28500吨,且全部分类处理,那么每天回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元
(1)求每台A型加湿器和B型加湿器的销售利润;
(2)该商店计划一次购进两种型号的加湿器共100台,其中B型加湿器的进货量不超过A型加湿器的2倍,设购进A型加湿器x台.这100台加湿器的销售总利润为y元
①求y关于x的函数关系式;
②该商店应怎样进货才能使销售总利润最大?
(3)实际进货时,厂家对A型加湿器出厂价下调m(0<m<100)元,且限定商店最多购进A型加湿器70台,若商店保持两种加湿器的售价不变,请你根据以上信息及(2)中条件,设计出使这100台加湿器销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级有学生400人,为了解这个年级普及安全教育的情况,随机抽取了20名学生,进行安全教育考试,测试成绩(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)请补全七年级20名学生安全教育测试成绩频数分布直方图;
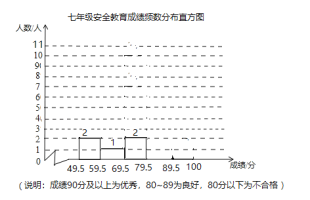
(2)样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 85.4 |
|
|
|
(3)估计七年级成绩优秀的学生人数约为_________人.
(4)学校有安全教育老师男女各2名,现从这4名老师中随机挑选2名参加“安全教育”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.

已知:如图,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() ,使直线
,使直线![]() 直线
直线![]() .
.
作法:如图,
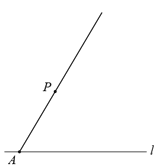
①在直线![]() 上任取一点
上任取一点![]() ,作射线
,作射线![]() ;
;
②以![]() 为圆心,
为圆心,![]() 为半径作弧,交直线
为半径作弧,交直线![]() 于点
于点![]() ,连接
,连接![]() ;
;
③以![]() 为圆心,
为圆心,![]() 长为半径作弧,交射线
长为半径作弧,交射线![]() 于点
于点![]() ;分别以
;分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,在
长为半径作弧,在![]() 的右侧两弧交于点
的右侧两弧交于点![]() ;
;
④作直线![]() ;
;
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依据1).
.(_______________________________)(填依据1).
![]() ,
,
![]() .
.
![]() ,∴直线
,∴直线![]() 直线
直线![]() .(______________________)(填依据2).
.(______________________)(填依据2).
查看答案和解析>>
科目:初中数学 来源: 题型:
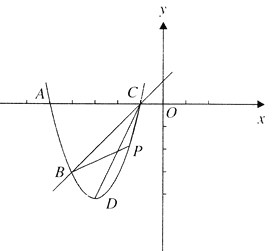
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为顶点,
为顶点,![]() 为抛物线上一动点(与点
为抛物线上一动点(与点![]() 不重合)
不重合)
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
![]() 该抛物线上是否存在点
该抛物线上是否存在点![]() ,使
,使![]() ?若存在,求出所有点
?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com