
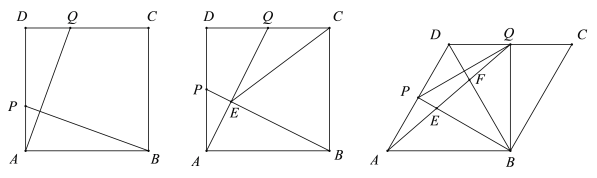
【题目】如图1,边长为6的正方形ABCD,动点P、Q各从点A,D同时出发,分别沿边AD,DC方向运动,且速度均为每秒1个单位长度.
(1)AQ与BP关系为________________;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,试探究∠CEQ和∠BCE满足怎样的数量关系;
(3)如图3,将正方形变为菱形且∠BAD=60°,其余条件不变,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
【答案】(1)AQ=BP且AQ⊥BP;(2)∠BCE=2∠CEQ;(3)![]() ;
;![]()
【解析】
(1)先利用“SAS”证得△ADQ≌△BAP,再利用角的计算,即可证得AQ⊥BP,AQ=BP;
(2)取AB中点为F,连结CF交BE于H,证得四边形QAFC是平行四边形,再证得CH所在直线是线段BE的中垂线,则CE=BC,从而求得∠BCE=2∠CEQ;
(3)先证得△BPQ为等边三角形,得到![]() ,当P到AD中点时,BP最短,从而得到S的最小值;作AM⊥CD于M,利用“SAS”证得△DPF≌△DQF,根据∠DPF=∠DQF即可求解.
,当P到AD中点时,BP最短,从而得到S的最小值;作AM⊥CD于M,利用“SAS”证得△DPF≌△DQF,根据∠DPF=∠DQF即可求解.
(1)AQ⊥BP,AQ=BP,理由如下:
∵动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度,
∴DQ=AP,
∵四边形ABCD是正方形,
∴AD=BA,∠ADQ=∠BAP=90°,
在△ADQ和△BAP中,
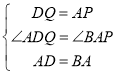 ,
,
∴△ADQ≌△BAP(SAS),
∴AQ=BP,且∠DAQ=∠ABP,
又∵∠DAQ+∠BAQ=90°,
∴∠ABP+∠BAQ=90°,
∴∠AEB=90°,
即AQ⊥BP;

(2)证明:取AB中点为F,连结CF交BE于H,
∵四边形ABCD是边长为6的正方形,
∴CD∥AB,
∵DQ=CQ=3,AF=FB=3,
∴CQ= AF,
∴四边形QAFC是平行四边形,
∴CF∥AQ,
∵AQ⊥BP,
∴CF⊥BP,
∵FH∥AE,且F为AB中点,
∴H为EB中点,即BH=EH,
∴CH所在直线是线段BE的中垂线,
∴CE=CB,
∴∠ECH=∠BCH,
∵CH∥AQ,
∴∠HCE=∠QEC,
∴∠BCE=2∠ECH=2∠CEQ,
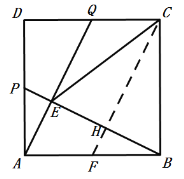
(3)∵四边形ABCD是菱形,且∠BAD=60°,
∴AD=AB,CD∥AB,
∴△ABD为等边三角形,∠DBA=∠BDQ,
∴∠BAP=∠BDQ=60°,BD=BA,
∵动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度,
∴DQ=AP,
在△BDQ和△BAP中,
 ,
,
∴△BDQ≌△BAP(SAS),
∴BQ=BP,且∠DBQ=∠ABP,
又∵∠ABP +∠PBD=60°,
∴∠DBQ +∠PBD =60°,即∠PBQ=60°,
∴△BPQ为等边三角形,
作QG⊥BP于G,
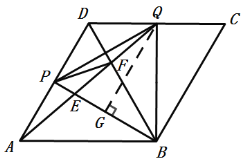
∴![]() ,
,
∴![]() ,
,
当且仅当BP⊥AD时,即P到AD中点时,BP最短,
BP![]() ,
,
∴![]() ,
,
连结PF,过点A作AM⊥CD交CD延长线于M,

∵AP=PD=DQ=![]() AD=3,
AD=3,
在△DPF和△DQF中,
 ,
,
∴△DPF≌△DQF(SAS),
在Rt△ADM中,AD=6,∠ADM=180![]() -∠ADB-∠QDB =60°,
-∠ADB-∠QDB =60°,
∴![]() ,
,![]() ,
,
∴tan∠DPF=tan∠DQF=![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
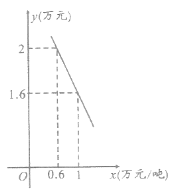
【题目】某蔬菜批发公司用实际行动支持抗击新冠肺炎疫情,为确保市民在疫情期间的蔬菜供应,以平均每吨![]() 万元的价格购进一批蔬菜,已知这批蔬菜通过网络在市场上的日销售量
万元的价格购进一批蔬菜,已知这批蔬菜通过网络在市场上的日销售量![]() (吨)与销售价格
(吨)与销售价格![]() (万元/吨)之间的函数关系如下图所示.
(万元/吨)之间的函数关系如下图所示.
(1)求日销售量![]() 与销售价格
与销售价格![]() 之间的函数关系式; (不要求写
之间的函数关系式; (不要求写![]() 的取值范围)
的取值范围)
(2)如果要确保日销售量不小于![]() 吨,求最大毛利润.(假设:毛利润=销售额-购进成本)
吨,求最大毛利润.(假设:毛利润=销售额-购进成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
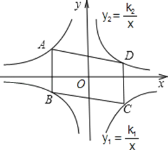
【题目】如图,平行四边形ABCD的顶点为A、C在双曲线y1=![]() 上,B、D在双曲线
上,B、D在双曲线![]() 上,k1=2k2(k1>0),AB∥y轴,
上,k1=2k2(k1>0),AB∥y轴,![]() =24,则k2的值为( )
=24,则k2的值为( )
A.4B.-4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知
,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知![]() .
.
(1)求证:AD是⊙O的切线;
(2)若BC=8,![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级教师对试卷讲评课中学生参与的深度和广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
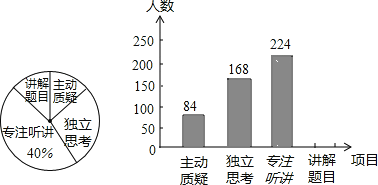
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有12000名初中学生,那么在试卷讲评课中,独立思考的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
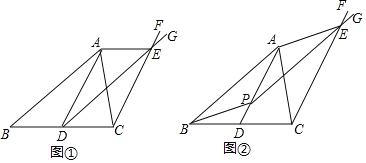
【题目】如图,AD是△ABC的中线,过点C作直线CF∥AD.
(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.
(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.
(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
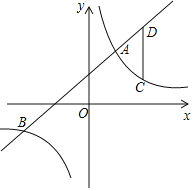
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(1)求一次函数和反比例函数的表达式;
(2)点C是第一象限内反比例函数图象上的一点,且点C在A的右侧,过点C作CD平行于y轴交直线AB于点D,若以C为圆心,CD长为半径的⊙C恰好与y轴相切,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
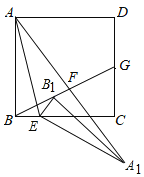
【题目】如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
(1)求证:△AA1E∽△BB1E;
(2)延长BB1分别交线段AA1,DC于点F、G,求证:AF=A1F;
(3)在(2)的条件下,若AB=4,BE=1,G是DC的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
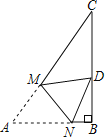
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com