
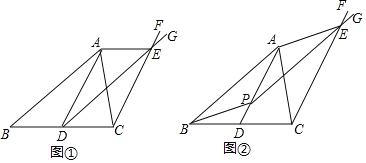
【题目】如图,AD是△ABC的中线,过点C作直线CF∥AD.
(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.
(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.
(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.
【答案】【问题】:详见解析;【探究】:四边形ABPE是平行四边形,理由详见解析;【应用】:8.
【解析】
(1)先根据平行线的性质和等量代换得出∠1=∠3,再利用中线性质得到BD=DC,证明△ABD≌△EDC,从而证明AB=DE(2)方法一:过点D作DN∥PE交直线CF于点N,由平行线性质得出四边形PDNE是平行四边形,从而得到四边形ABPE是平行四边形.方法二: 延长BP交直线CF于点N,根据平行线的性质结合等量代换证明△ABP≌△EPN,
从而证明四边形ABPE是平行四边形(3)延长BP交CF于H,根据平行四边形的性质结合三角形的面积公式求解即可.
证明:如图①
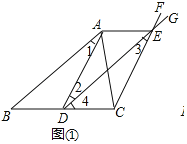
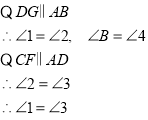
![]() 是
是![]() 的中线,
的中线,
![]()
![]()
![]()
(或证明四边形ABDE是平行四边形,从而得到![]() )
)
【探究】
四边形ABPE是平行四边形.
方法一:如图②,
证明:过点D作![]() 交直线
交直线![]() 于点
于点![]() ,
,

![]()
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
∵由问题结论可得![]()
![]()
∴四边形![]() 是平行四边形.
是平行四边形.
方法二:如图③,
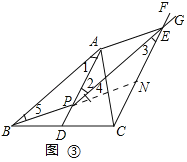
证明:延长BP交直线CF于点N,
![]()
![]()
![]()
![]()
![]()
∵![]() 是
是![]() 的中线,
的中线,![]()
![]()
![]()
![]()
∴四边形![]() 是平行四边形.
是平行四边形.
【应用】
如图④,延长BP交CF于H.
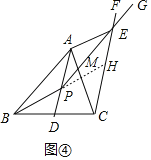
由上面可知,四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
∴四边形APHE是平行四边形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()


科目:初中数学 来源: 题型:
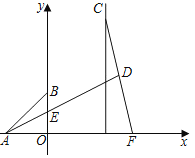
【题目】如图,A、B两点的坐标分别为(﹣4,0),(0,4),C、F分别是直线x=6和x轴上的动点,CF=12,D是CF的中点,连接AD交y轴与点E,△ABE面积的最小值为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),请你直接写出BM、DN和MN的数量关系:__________.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请写出直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
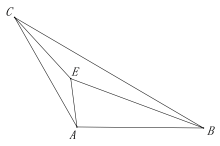
【题目】如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC 内一点,且满足![]() 则点E 在运动过程中所形成的图形的长为 ( )
则点E 在运动过程中所形成的图形的长为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
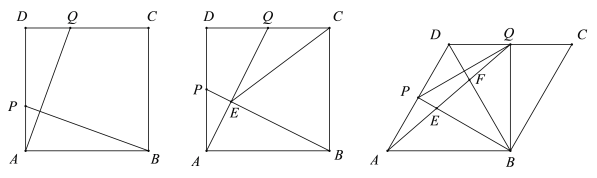
【题目】如图1,边长为6的正方形ABCD,动点P、Q各从点A,D同时出发,分别沿边AD,DC方向运动,且速度均为每秒1个单位长度.
(1)AQ与BP关系为________________;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,试探究∠CEQ和∠BCE满足怎样的数量关系;
(3)如图3,将正方形变为菱形且∠BAD=60°,其余条件不变,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州融创乐园是国内首个以南越文化、岭南风格为主题的游乐园,自2019年6月开园以来受到了国内外游客的热捧.某旅游团组织一批游客游玩了乐园内的四个网红项目,“A.双龙飞舞”、“B.飞跃广东”、“C.云霄塔”、“D.怒海狂涛”,并进行了“我最喜欢的一个项目”的投票评选活动,投票结果绘制成以下两幅尚未完整的统计图.请你根据图中提供的信息,解答下列问题:
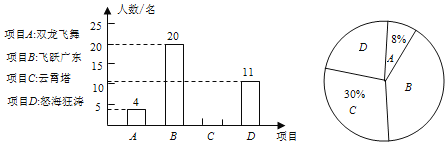
(1)参与投票的游客总人数为 人;
(2)扇形统计图中B所对的圆心角度数为 度,并补全条形统计图;
(3)从投票给“双龙飞舞“的3名男生和1名女生中随机抽取2名了解情况,请你用列举法求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=![]() ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
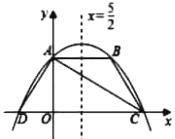
A.点B坐标为(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
查看答案和解析>>
科目:初中数学 来源: 题型:
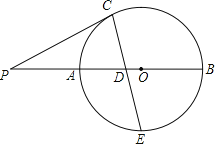
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
(1)求证:PC是⊙O的切线;
(2)求证:CDDE=2ODPD;
(3)若AB=8,CDDE=15,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元
(1)求每台A型加湿器和B型加湿器的销售利润;
(2)该商店计划一次购进两种型号的加湿器共100台,其中B型加湿器的进货量不超过A型加湿器的2倍,设购进A型加湿器x台.这100台加湿器的销售总利润为y元
①求y关于x的函数关系式;
②该商店应怎样进货才能使销售总利润最大?
(3)实际进货时,厂家对A型加湿器出厂价下调m(0<m<100)元,且限定商店最多购进A型加湿器70台,若商店保持两种加湿器的售价不变,请你根据以上信息及(2)中条件,设计出使这100台加湿器销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com