
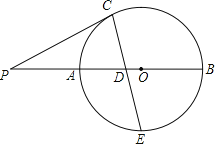
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
(1)求证:PC是⊙O的切线;
(2)求证:CDDE=2ODPD;
(3)若AB=8,CDDE=15,求PA的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OC,OE,根据等腰三角形的性质得到∠E=∠OCE,求得∠E+∠ODE=90°,得到∠PCD=∠ODE,得到OC⊥PC,于是得到结论;
(2)连接AC,BE,BC,根据相似三角形的性质得到![]() ,推出CDDE=AO2﹣OD2;由△ACP∽△CBP,得到
,推出CDDE=AO2﹣OD2;由△ACP∽△CBP,得到![]() =
=![]() ,
,
得到PD2=PD2+2PDOD+OD2﹣OA2,于是得到结论;
(3)由(2)知,CDDE=AO2﹣OD2;把已知条件代入得到OD=1(负值舍去),求得AD=3,由(2)知,CDDE=2ODPD,于是得到结论.
(1)证明:连接OC,OE,
∵OC=OE,
∴∠E=∠OCE,
∵E是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴∠AOE=∠BOE=90°,
∴∠E+∠ODE=90°,
∵PC=PD,
∴∠PCD=∠PDC,
∵∠PDC=∠ODE,
∴∠PCD=∠ODE,
∴∠PCD+∠OCD=∠ODE+∠E=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)证明:连接AC,BE,BC,
∵∠ACD=∠DBE,∠CAD=∠DEB,
∴△ACD∽△EBD,
∴![]() ,
,
∴CDDE=ADBD=(AO﹣OD)(AO+OD)=AO2﹣OD2;
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠PCO=90°,
∴∠ACP+∠ACO=∠ACO+∠BCO=90°,
∴∠ACP=∠BCO,
∵∠BCO=∠CBO,
∴∠ACP=∠PBC,
∵∠P=∠P,
∴△ACP∽△CBP,
∴![]() =
=![]()
∴PC2=PBPA=(PD+DB)(PD﹣AD)=(PD+OD+OA)(PD+OD﹣OA)=(PD+OD)2﹣OA2=PD2+2PDOD+OD2﹣OA2,
∵PC=PD,
∴PD2=PD2+2PDOD+OD2﹣OA2,
∴OA2﹣OD2=2ODPD,
<>∴CDDE=2ODPD;(3)解:∵AB=8,
∴OA=4,
由(2)知,CDDE=AO2﹣OD2;
∵CDDE=15,
∴15=42﹣OD2,
∴OD=1(负值舍去),
∴AD=3,
由(2)知,CDDE=2ODPD,
∴PD=![]() =
=![]() ,
,
∴PA=PD﹣AD=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
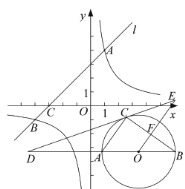
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
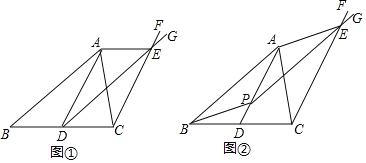
【题目】如图,AD是△ABC的中线,过点C作直线CF∥AD.
(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.
(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.
(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现![]() 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.
是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
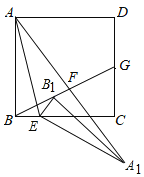
【题目】如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
(1)求证:△AA1E∽△BB1E;
(2)延长BB1分别交线段AA1,DC于点F、G,求证:AF=A1F;
(3)在(2)的条件下,若AB=4,BE=1,G是DC的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.
a.教育未来指数得分的频数分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
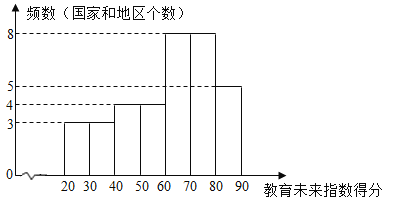
b.教育未来指数得分在![]() 这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
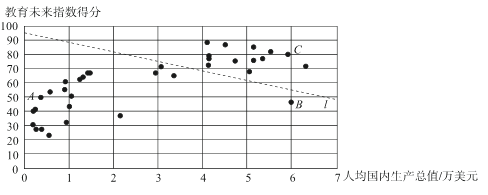
c.35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图如下:
d.中国和中国香港的教育未来指数得分分别为32.9和68.5.
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第______;
(2)在35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○”画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为_____万美元;(结果保留一位小数)
(4)下列推断合理的是__________.(只填序号即可)
①相较于点![]() 所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
②相较于点![]() 所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A.
求作:![]() ,使得
,使得![]() .
.
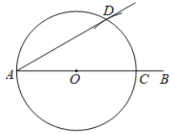
作法:如图,
(1)作射线![]() ;
;
(2)在射线![]() 取一点O,以O为圆心,
取一点O,以O为圆心,![]() 为半径作圆,与射线
为半径作圆,与射线![]() 相交于点C;
相交于点C;
(3)以C为圆心,![]() C为半径作弧,与
C为半径作弧,与![]() 交于点D,作射线
交于点D,作射线![]() .
.
则![]() 即为所求的角.
即为所求的角.
请回答:该尺规作图的依据是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)求点![]() 坐标;
坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 及抛物线在
及抛物线在![]() 两点之间的部分围成的封闭区域(不含边界)记为
两点之间的部分围成的封闭区域(不含边界)记为![]() .
.
①当![]() 时,结合函数图象,直接写出区域
时,结合函数图象,直接写出区域![]() 内的整点个数;
内的整点个数;
②如果区域![]() 内有2个整点,请求出
内有2个整点,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com