
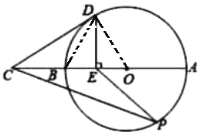
°æƒø°øπ≈œ£¿∞ ˝—ߺ“±œ¥Ô∏Á¿≠Àπ»œŒ™£∫°∞“ª«–∆Ω√ÊÕº–Œ÷–◊Ó√¿µƒ «‘≤°±£Æ«Î—–æø»Áœ¬√¿¿ˆµƒ‘≤£Æ»ÁÕº£¨œfl∂ŒAB «°—Oµƒ÷±æ∂£¨—”≥§AB÷¡µ„C£¨ πBC£ΩOB£¨µ„E «œfl∂ŒOBµƒ÷–µ„£¨DE°ÕABΩª°—O”⁄µ„D£¨µ„P «°—O…œ“ª∂ص„£®≤ª”ε„A£¨B÷ÿ∫œ£©£¨¡¨Ω”CD£¨PE£¨PC£Æ
£®1£©«Û÷§£∫CD «°—Oµƒ«–œfl£ª
£®2£©–°√˜‘⁄—–æøµƒπ˝≥Ã÷–∑¢œ÷![]() «“ª∏ˆ»∑∂®µƒ÷µ£Æªÿ¥’‚∏ˆ»∑∂®µƒ÷µ «∂‡…Ÿ£ø≤¢∂‘–°√˜∑¢œ÷µƒΩ·¬€º”“‘÷§√˜£Æ
«“ª∏ˆ»∑∂®µƒ÷µ£Æªÿ¥’‚∏ˆ»∑∂®µƒ÷µ «∂‡…Ÿ£ø≤¢∂‘–°√˜∑¢œ÷µƒΩ·¬€º”“‘÷§√˜£Æ

°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©![]() £¨Ω‚Œˆ
£¨Ω‚Œˆ
°æΩ‚Œˆ°ø
±æÂøº≤È¡À«–œflµƒ≈–∂®”Ζ‘÷ º∞œ‡À∆»˝Ω«–Œµƒ≈–∂®”Ζ‘÷ £Æ£®1£©¡¨Ω”OD£¨DB£¨”…“—÷™ø…µ√DE¥π÷±∆Ω∑÷OB£¨”⁄ «DB£ΩDO£¨∂¯OB£ΩOD£¨À˘“‘DB£ΩDO£ΩOB£¨º¥°˜ODB «µ»±fl»˝Ω«–Œ£¨”⁄ «°œBDO£Ω60°„£¨‘Ÿ”…µ»—¸»˝Ω«–Œµƒ–‘÷ º∞»˝Ω«–ŒµƒÕ‚Ω«–‘÷ ø…µ√°œCDB£Ω30°„£¨¥”∂¯ø…µ√°œODC£Ω90°„£¨À˘“‘OD°ÕCD£¨À˘“‘CD «°—Oµƒ«–œfl£ª£®2£©¡¨Ω”OP£¨”…“—÷™Ãıº˛µ√OP£ΩOB£ΩBC£Ω2OE£¨‘Ÿ¿˚”√°∞¡Ω◊ȱfl≥…±»¿˝£¨º–Ω«œ‡µ»°±÷§√˜°˜OEP°◊°˜OPC£¨◊Ó∫Û”…œ‡À∆»˝Ω«–Œµƒ∂‘”¶±fl≥…±»¿˝µ√µΩΩ·¬€£Æ
Ω‚£∫£®1£©»Á¥Õº£¨¡¨Ω”OD£¨DB£¨°flµ„E «œfl∂ŒOBµƒ÷–µ„£¨DE°ÕABΩª°—O”⁄µ„D£¨°‡DE¥π÷±∆Ω∑÷OB£¨°‡DB£ΩDO£Æ°flDO£ΩOB£¨°‡DB£ΩDO£ΩOB£¨°‡°˜ODB «µ»±fl»˝Ω«–Œ£¨°‡°œBDO£Ω°œDBO£Ω60°„£Æ°flBC£ΩOB£ΩBD£¨«“°œDBEŒ™°˜BDCµƒÕ‚Ω«£¨°‡°œBCD£Ω°œBDC£Ω![]() °œDBO£Æ°fl°œDBO£Ω60°„£¨°‡°œCDB£Ω30°„£Æ°‡°œODC£Ω°œBDO£´°œBDC£Ω60°„£´30°„£Ω90°„£¨°‡OD°ÕCD£¨°‡CD «°—Oµƒ«–œfl£ª
°œDBO£Æ°fl°œDBO£Ω60°„£¨°‡°œCDB£Ω30°„£Æ°‡°œODC£Ω°œBDO£´°œBDC£Ω60°„£´30°„£Ω90°„£¨°‡OD°ÕCD£¨°‡CD «°—Oµƒ«–œfl£ª
£®2£©’‚∏ˆ»∑∂®µƒ÷µ «![]() £Æ
£Æ
÷§√˜£∫»Á¥Õº£¨¡¨Ω”OP£¨°flOP£ΩOB£ΩBC£Ω2OE£¨°‡![]() £Ω
£Ω![]() £Ω
£Ω![]() £¨”÷°fl°œCOP£Ω°œPOE£¨°‡°˜OEP°◊°˜OPC£¨°‡
£¨”÷°fl°œCOP£Ω°œPOE£¨°‡°˜OEP°◊°˜OPC£¨°‡![]() £Ω
£Ω![]() £Ω
£Ω![]() £Æ
£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨≈◊ŒÔœfly£Ω![]() m”Îy÷·Ωª”⁄µ„C£¨”Îx÷·Ωª”⁄µ„A∫Õµ„B£®∆‰÷–µ„A‘⁄y÷·◊Û≤‡£¨µ„B‘⁄y÷·”“≤‡£©£Æ
m”Îy÷·Ωª”⁄µ„C£¨”Îx÷·Ωª”⁄µ„A∫Õµ„B£®∆‰÷–µ„A‘⁄y÷·◊Û≤‡£¨µ„B‘⁄y÷·”“≤‡£©£Æ
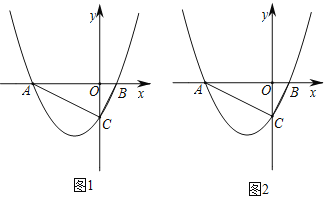
£®1£©»Ù≈◊ŒÔœfly£Ω![]() mµƒ∂‘≥∆÷·Œ™÷±œflx£Ω1£¨«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
mµƒ∂‘≥∆÷·Œ™÷±œflx£Ω1£¨«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº1£¨°œACB£Ω90°„£¨µ„P «≈◊ŒÔœfly£Ω![]() m…œµƒ“ªµ„£¨»ÙS°˜BCP£Ω
m…œµƒ“ªµ„£¨»ÙS°˜BCP£Ω![]() £¨«Ûµ„Pµƒ◊¯±Í£ª
£¨«Ûµ„Pµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨π˝µ„A◊˜AD°ŒBCΩª≈◊ŒÔœfl”⁄µ„D£¨»Ùµ„Dµƒ◊›◊¯±ÍŒ™©Å![]() m£¨«Û÷±œflADµƒΩ‚Œˆ Ω£Æ
m£¨«Û÷±œflADµƒΩ‚Œˆ Ω£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œCAB£Ω120°„£¨AB£ΩAC£Ω3£¨µ„E «»˝Ω«–ŒABC ƒ⁄“ªµ„£¨«“¬˙◊„![]() ‘Úµ„E ‘⁄‘À∂Øπ˝≥Ã÷–À˘–Œ≥…µƒÕº–Œµƒ≥§Œ™ £® £©
‘Úµ„E ‘⁄‘À∂Øπ˝≥Ã÷–À˘–Œ≥…µƒÕº–Œµƒ≥§Œ™ £® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ„÷›»⁄¥¥¿÷‘∞ «π˙ƒ⁄ ◊∏ˆ“‘ƒœ‘ΩŒƒªØ°¢¡Îƒœ∑Á∏ÒŒ™÷˜Ã‚µƒ”Œ¿÷‘∞£¨◊‘2019ƒÍ6‘¬ø™‘∞“‘¿¥ ‹µΩ¡Àπ˙ƒ⁄Õ‚”ŒøÕµƒ»»≈ı£Æƒ≥¬√”ŒÕ≈◊È÷Ø“ª≈˙”ŒøÕ”ŒÕÊ¡À¿÷‘∞ƒ⁄µƒÀƒ∏ˆÕ¯∫ϜӃø£¨°∞A£ÆÀ´¡˙∑…ŒË°±°¢°∞B£Æ∑…‘æπ„∂´°±°¢°∞C£Æ‘∆œˆÀ˛°±°¢°∞D£Æ≈≠∫£øÒÃŒ°±£¨≤¢Ω¯––¡À°∞Œ“◊Óœ≤ª∂µƒ“ª∏ˆœÓƒø°±µƒÕ∂∆±∆¿—°ªÓ∂Ø£¨Õ∂∆±Ω·π˚ªÊ÷∆≥…“‘œ¬¡Ω∑˘…–Œ¥ÕÍ’˚µƒÕ≥º∆Õº£Æ«Îƒ„∏˘æ›Õº÷–Ã·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
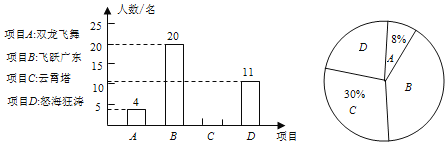
£®1£©≤Œ”ÎÕ∂∆±µƒ”ŒøÕ◊‹»À ˝Œ™°° °°»À£ª
£®2£©…»–ŒÕ≥º∆Õº÷–BÀ˘∂‘µƒ‘≤–ƒΩ«∂» ˝Œ™°° °°∂»£¨≤¢≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©¥”Õ∂∆±∏¯°∞À´¡˙∑…ŒË°∞µƒ3√˚ƒ–…˙∫Õ1√˚≈Æ…˙÷–Àʪ˙≥È»°2√˚¡ÀΩ‚«Èøˆ£¨«Îƒ„”√¡–æŸ∑®«Û«°∫√≥ȵΩ1ƒ–1≈Ƶƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœfly£Ωax2£´bx£´4Ωªy÷·”⁄µ„A£¨Ωªπ˝µ„A«“∆Ω––”⁄x÷·µƒ÷±œfl”⁄¡Ì“ªµ„B£¨Ωªx÷·”⁄C£¨D¡Ωµ„£®µ„C‘⁄µ„D”“±fl£©£¨∂‘≥∆÷·Œ™÷±œflx£Ω![]() £¨¡¨Ω”AC£¨AD£¨BC£Æ»Ùµ„Bπÿ”⁄÷±œflACµƒ∂‘≥∆µ„«°∫√¬‰‘⁄œfl∂ŒOC…œ£¨œ¬¡–Ω·¬€÷–¥ÌŒÛµƒ «£® £©
£¨¡¨Ω”AC£¨AD£¨BC£Æ»Ùµ„Bπÿ”⁄÷±œflACµƒ∂‘≥∆µ„«°∫√¬‰‘⁄œfl∂ŒOC…œ£¨œ¬¡–Ω·¬€÷–¥ÌŒÛµƒ «£® £©
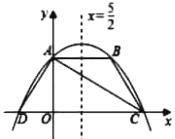
A.µ„B◊¯±ÍŒ™(5£¨4)B.AB£ΩADC.a£Ω![]() D.OCOD£Ω16
D.OCOD£Ω16
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
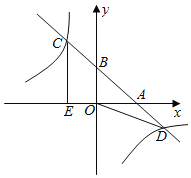
°æƒø°ø»ÁÕº£¨÷±œfly£Ω©Åx+b”Îx°¢y÷·µƒ’˝∞Î÷·Ωª”⁄µ„A£¨B£¨”ÎÀ´«˙œfly£Ω©Å![]() Ωª”⁄µ„C£®µ„C‘⁄µ⁄∂˛œÛœfiƒ⁄£©£¨µ„D£¨π˝µ„C◊˜CE°Õx÷·”⁄µ„E£¨º«Àƒ±fl–ŒOBCEµƒ√ʪ˝Œ™S1£¨°˜OBDµƒ√ʪ˝Œ™S2£¨»Ù
Ωª”⁄µ„C£®µ„C‘⁄µ⁄∂˛œÛœfiƒ⁄£©£¨µ„D£¨π˝µ„C◊˜CE°Õx÷·”⁄µ„E£¨º«Àƒ±fl–ŒOBCEµƒ√ʪ˝Œ™S1£¨°˜OBDµƒ√ʪ˝Œ™S2£¨»Ù![]() £Ω
£Ω![]() £¨‘Úbµƒ÷µŒ™_____£Æ
£¨‘Úbµƒ÷µŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
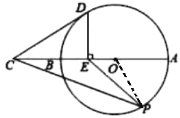
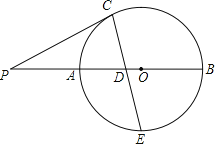
°æƒø°ø»ÁÕº£¨ABŒ™°—Oµƒ÷±æ∂£¨PŒ™BA—”≥§œfl…œ“ªµ„£¨µ„C‘⁄°—O…œ£¨¡¨Ω”PC£¨DŒ™∞Îæ∂OA…œ“ªµ„£¨PD£ΩPC£¨¡¨Ω”CD≤¢—”≥§Ωª°—O”⁄µ„E£¨«“E «![]() µƒ÷–µ„£Æ
µƒ÷–µ„£Æ
£®1£©«Û÷§£∫PC «°—Oµƒ«–œfl£ª
£®2£©«Û÷§£∫CDDE£Ω2ODPD£ª
£®3£©»ÙAB£Ω8£¨CDDE£Ω15£¨«ÛPAµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ„CŒ™œfl∂Œ![]() …œ“ªµ„£¨“‘
…œ“ªµ„£¨“‘![]() Œ™–±±fl◊˜µ»—¸
Œ™–±±fl◊˜µ»—¸![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨‘⁄
£¨‘⁄![]() Õ‚≤‡£¨“‘
Õ‚≤‡£¨“‘![]() Œ™–±±fl◊˜µ»—¸
Œ™–±±fl◊˜µ»—¸![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
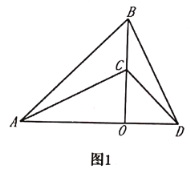
£®1£©»ÁÕº1£¨µ±![]() ±£∫
±£∫
¢Ÿ«Û÷§£∫![]() £ª
£ª
¢⁄≈–∂œœfl∂Œ![]() ”Î
”Î![]() µƒ ˝¡øπÿœµ£¨≤¢÷§√˜£ª
µƒ ˝¡øπÿœµ£¨≤¢÷§√˜£ª
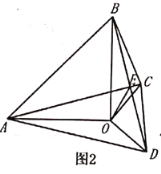
£®2£©»ÁÕº2£¨µ±![]() ±£¨
±£¨![]() ”Î
”Î![]() µƒ ˝¡øπÿœµ «∑Ò±£≥÷≤ª±‰£ø
µƒ ˝¡øπÿœµ «∑Ò±£≥÷≤ª±‰£ø
∂‘”⁄“‘…œŒ £¨–°ƒ¡Õ¨—ßÕ®π˝π€≤Ï°¢ µ—È£¨–Œ≥…¡ÀΩ‚æˆ∏√Œ µƒº∏÷÷Àº¬∑£∫
œÎ∑®1£∫≥¢ ‘Ω´µ„DŒ™–˝◊™÷––ƒ£¨π˝µ„D◊˜œfl∂Œ![]() ¥πœfl£¨Ωª
¥πœfl£¨Ωª![]() —”≥§œfl”⁄µ„G£¨¡¨Ω”
—”≥§œfl”⁄µ„G£¨¡¨Ω”![]() £ªÕ®π˝÷§√˜
£ªÕ®π˝÷§√˜![]() Ω‚æˆ“‘…œŒ £ª
Ω‚æˆ“‘…œŒ £ª
œÎ∑®2£∫≥¢ ‘Ω´µ„DŒ™–˝◊™÷––ƒ£¨π˝µ„D◊˜œfl∂Œ![]() ¥πœfl£¨¥π◊„Œ™µ„G£¨¡¨Ω”
¥πœfl£¨¥π◊„Œ™µ„G£¨¡¨Ω”![]() £ÆÕ®π˝÷§√˜
£ÆÕ®π˝÷§√˜![]() Ω‚æˆ“‘…œŒ £ª
Ω‚æˆ“‘…œŒ £ª
œÎ∑®3£∫≥¢ ‘¿˚”√Àƒµ„π≤‘≤£¨π˝µ„D◊˜![]() ¥πœfl∂Œ
¥πœfl∂Œ![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨Õ®π˝÷§√˜D°¢F°¢B°¢EÀƒµ„π≤‘≤£¨¿˚”√‘≤µƒœ‡πÿ÷™ ∂Ω‚æˆ“‘…œŒ £Æ
£¨Õ®π˝÷§√˜D°¢F°¢B°¢EÀƒµ„π≤‘≤£¨¿˚”√‘≤µƒœ‡πÿ÷™ ∂Ω‚æˆ“‘…œŒ £Æ
«Îƒ„≤Œøº…œ√ʵƒœÎ∑®£¨÷§√˜![]() £®“ª÷÷∑Ω∑®º¥ø…£©£Æ
£®“ª÷÷∑Ω∑®º¥ø…£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
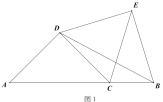
°æƒø°øΩ´“ª¥Û°¢“ª–°¡Ω∏ˆµ»—¸÷±Ω«»˝Ω«–Œ∆¥‘⁄“ª∆£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
£®1£©»ÁÕº1,»Ù![]() »˝µ„‘⁄Õ¨“ªÃı÷±œfl…œ£¨‘Ú
»˝µ„‘⁄Õ¨“ªÃı÷±œfl…œ£¨‘Ú![]() ”Î
”Î![]() µƒπÿœµ « £ª
µƒπÿœµ « £ª
£®2£©»ÁÕº2£¨»Ù![]() »˝µ„≤ª‘⁄Õ¨“ªÃı÷±œfl…œ,
»˝µ„≤ª‘⁄Õ¨“ªÃı÷±œfl…œ,![]() ”Î
”Î![]() œ‡Ωª”⁄µ„
œ‡Ωª”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() ,≤¬œÎ
,≤¬œÎ![]() ÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢∏¯”Ë÷§√˜£ª
÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢∏¯”Ë÷§√˜£ª
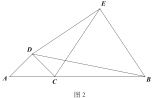
£®3£©»ÁÕº3£¨‘⁄(2)µƒÃıº˛œ¬◊˜![]() µƒ÷–µ„
µƒ÷–µ„![]() ,¡¨Ω”
,¡¨Ω”![]() £¨÷±Ω”–¥≥ˆ
£¨÷±Ω”–¥≥ˆ![]() ”Î
”Î![]() ÷ƺ‰µƒπÿœµ£Æ
÷ƺ‰µƒπÿœµ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com