
【题目】点C为线段![]() 上一点,以
上一点,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,在
,在![]() 外侧,以
外侧,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() .
.
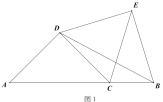
(1)如图1,当![]() 时:
时:
①求证:![]() ;
;
②判断线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
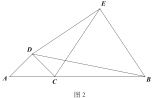
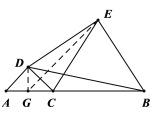
(2)如图2,当![]() 时,
时,![]() 与
与![]() 的数量关系是否保持不变?
的数量关系是否保持不变?
对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:
想法1:尝试将点D为旋转中心,过点D作线段![]() 垂线,交
垂线,交![]() 延长线于点G,连接
延长线于点G,连接![]() ;通过证明
;通过证明![]() 解决以上问题;
解决以上问题;
想法2:尝试将点D为旋转中心,过点D作线段![]() 垂线,垂足为点G,连接
垂线,垂足为点G,连接![]() .通过证明
.通过证明![]() 解决以上问题;
解决以上问题;
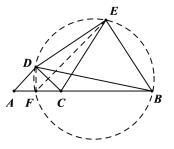
想法3:尝试利用四点共圆,过点D作![]() 垂线段
垂线段![]() ,连接
,连接![]() ,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
请你参考上面的想法,证明![]() (一种方法即可).
(一种方法即可).
【答案】(1)①证明见解析;②![]() ,证明见解析;(2)证明见解析.
,证明见解析;(2)证明见解析.
【解析】
(1)①如图(见解析),先根据直角三角形的性质得出![]() ,再根据等腰三角形的三线合一得出
,再根据等腰三角形的三线合一得出![]() 是斜边AC上的中线,然后根据直角三角形的性质
是斜边AC上的中线,然后根据直角三角形的性质![]() ,最后根据等量代换即可得证;
,最后根据等量代换即可得证;
②先结合①的结论、等腰直角三角形的性质![]() ,
,![]() ,
,![]() ,再根据角的和差、直角三角形的性质得出
,再根据角的和差、直角三角形的性质得出![]() ,然后根据等边三角形的判定与性质得出
,然后根据等边三角形的判定与性质得出![]() ,由此即可证出
,由此即可证出![]() ;
;
(2)想法1:先根据等腰三角形的性质、角的和差得出![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,从而可得
,从而可得![]() ,最后根据直角三角形斜边上的中线等于斜边的一半即可得证;
,最后根据直角三角形斜边上的中线等于斜边的一半即可得证;
想法2:先根据等腰直角三角形的性质、角的和差得出![]() ,
,![]() ,再根据相似三角形的判定与性质得出
,再根据相似三角形的判定与性质得出![]() ,从而可得
,从而可得![]() 平分
平分![]() ,然后根据等腰三角形的三线合一可得
,然后根据等腰三角形的三线合一可得![]() 是
是![]() 的垂直平分线,最后根据垂直平分线的性质、等量代换即可得证;
的垂直平分线,最后根据垂直平分线的性质、等量代换即可得证;
想法3:先根据垂直的定义、等腰直角三角形的定义得出![]() ,
,![]() ,从而可得
,从而可得![]() ,由此可证出D、F、B、E四点共圆,再根据圆周角定理可得
,由此可证出D、F、B、E四点共圆,再根据圆周角定理可得![]() ,然后同想法2的方法即可得证.
,然后同想法2的方法即可得证.
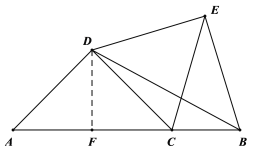
(1)①过点D作![]() 于F
于F
![]()
![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]() 是斜边AC上的中线(等腰三角形的三线合一)
是斜边AC上的中线(等腰三角形的三线合一)
![]()
![]() ;
;
②![]() ,证明如下:
,证明如下:
![]() 等腰
等腰![]() 与等腰
与等腰![]() 中
中![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
![]() ;
;
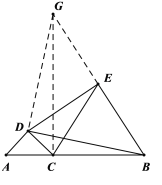
(2)想法1:如图,过点D作线段![]() 垂线,交
垂线,交![]() 延长线于点G,连接
延长线于点G,连接![]()
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]() ,即
,即![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
![]() 是直角三角形
是直角三角形
![]()
![]() 点E是BG的中点,即CE是斜边BG上的中线
点E是BG的中点,即CE是斜边BG上的中线
![]() ;
;
想法2:如图,过点D作线段![]() 垂线,垂足为点G,连接
垂线,垂足为点G,连接![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,即
,即![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,
,![]() ,
,![]() ,即
,即![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,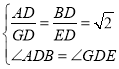
![]()
![]()
![]() 平分
平分![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() 是
是![]() 的垂直平分线(等腰三角形的三线合一)
的垂直平分线(等腰三角形的三线合一)
![]()
即![]() ;
;
想法3:如图,过点D作![]() 垂线段
垂线段![]() ,连接
,连接![]()
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,
,![]() ,
,![]()
![]()
![]() D、F、B、E四点共圆
D、F、B、E四点共圆
![]()
同想法2可证:![]() 是
是![]() 的垂直平分线
的垂直平分线
![]()
即![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现![]() 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.
是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.
a.教育未来指数得分的频数分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
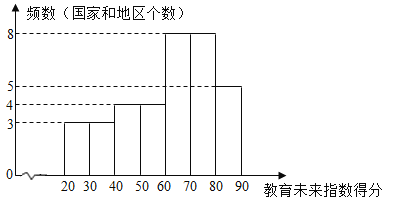
b.教育未来指数得分在![]() 这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c.35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图如下:
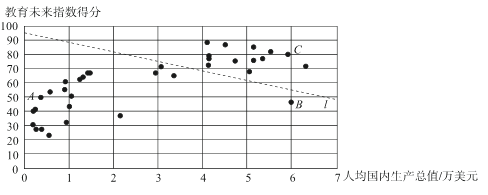
d.中国和中国香港的教育未来指数得分分别为32.9和68.5.
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第______;
(2)在35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○”画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为_____万美元;(结果保留一位小数)
(4)下列推断合理的是__________.(只填序号即可)
①相较于点![]() 所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
②相较于点![]() 所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A.
求作:![]() ,使得
,使得![]() .
.
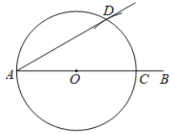
作法:如图,
(1)作射线![]() ;
;
(2)在射线![]() 取一点O,以O为圆心,
取一点O,以O为圆心,![]() 为半径作圆,与射线
为半径作圆,与射线![]() 相交于点C;
相交于点C;
(3)以C为圆心,![]() C为半径作弧,与
C为半径作弧,与![]() 交于点D,作射线
交于点D,作射线![]() .
.
则![]() 即为所求的角.
即为所求的角.
请回答:该尺规作图的依据是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
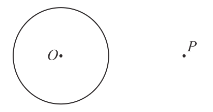
【题目】下面是小文设计的“过圆外一点作圆的切线”的作图过程.已知:![]() 和圆外一点
和圆外一点![]() .求作:过点
.求作:过点![]() 的
的![]() 的切线.作法:①连接
的切线.作法:①连接![]() ;②以
;②以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ;③作直线
;③作直线![]() ,
,![]() ;所以直线
;所以直线![]() ,
,![]() 为
为![]() 的切线.
的切线.
根据小文设计的作图过程,完成下面的证明.
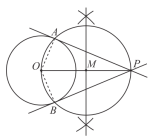
证明:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,
的直径,
∴![]() =∠________=________
=∠________=________
(________)(填推理的依据).
∴![]() ,________
,________![]() .
.
∵![]() ,
,![]() 为
为
∴直线![]() ,
,![]() 为
为![]() 的切线(________)(填推理的依据).
的切线(________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
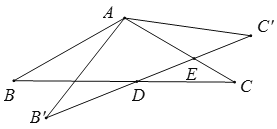
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.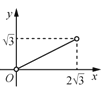 B.
B.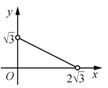 C.
C.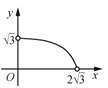 D.
D.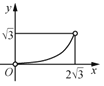
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com