
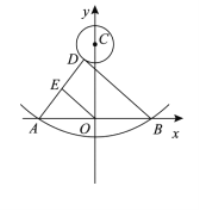
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆上的动点,
为半径的圆上的动点,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,则线段
,则线段![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 交
交![]() 轴负半轴)轴正半轴于
轴负半轴)轴正半轴于![]() 两点,
两点, ![]() 的面积为4.5;
的面积为4.5;
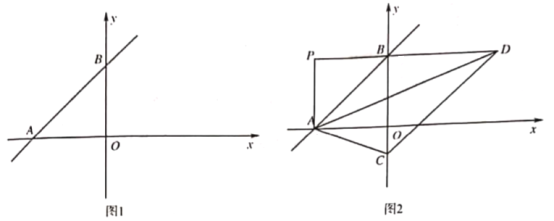
![]() 如图1.求
如图1.求![]() 的值;
的值;
![]() 如图2.在
如图2.在![]() 轴负半轴上取点
轴负半轴上取点![]() .点
.点![]() 在第一象限,
在第一象限,![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
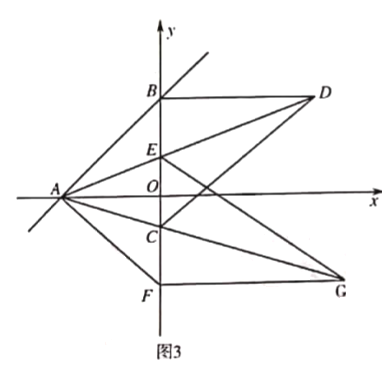
![]() 如图3,在
如图3,在![]() 的条件下.
的条件下.![]() 交
交![]() 轴于点
轴于点![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
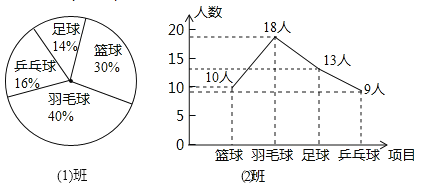
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
科目:初中数学 来源: 题型:
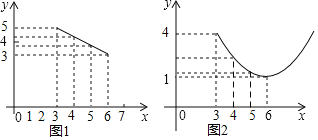
【题目】某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且![]() ,连接GO并延长交⊙O于点F,连接BF.
,连接GO并延长交⊙O于点F,连接BF.
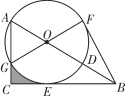
(1)求证:AO=AG;
(2)求证:BF是⊙O的切线;
(3)若BD=6,求图形中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com