
【题目】在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 交
交![]() 轴负半轴)轴正半轴于
轴负半轴)轴正半轴于![]() 两点,
两点, ![]() 的面积为4.5;
的面积为4.5;
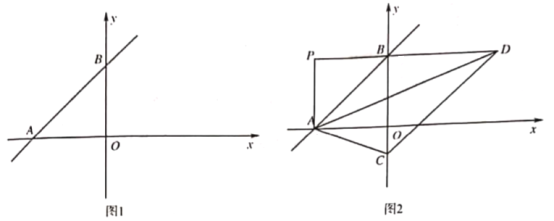
![]() 如图1.求
如图1.求![]() 的值;
的值;
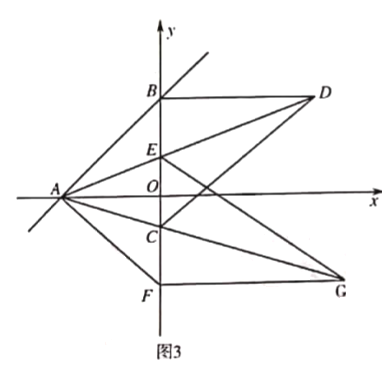
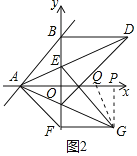
![]() 如图2.在
如图2.在![]() 轴负半轴上取点
轴负半轴上取点![]() .点
.点![]() 在第一象限,
在第一象限,![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如图3,在
如图3,在![]() 的条件下.
的条件下.![]() 交
交![]() 轴于点
轴于点![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)分别求![]() 、
、![]() 坐标,其中
坐标,其中![]() 的坐标用
的坐标用![]() 表示,利用
表示,利用![]() 为等量关系即求出
为等量关系即求出![]() 的值.
的值.
(2)由![]() 联想到在
联想到在![]() 上截取
上截取![]() ,则有
,则有![]() .由条件易证四边形
.由条件易证四边形![]() 是正方形,由
是正方形,由![]() 即得到
即得到![]() ,有
,有![]() ,
,![]() ,通过角度转换可得
,通过角度转换可得![]() .证
.证![]() ,即得到
,即得到![]() ,求得
,求得![]() .
.
(3)要求点![]() 坐标,即要求
坐标,即要求![]() 的长,又
的长,又![]() 在
在![]() 中,
中,![]() ,即求出
,即求出![]() 的长则
的长则![]() 确定,即求出
确定,即求出![]() .由
.由![]() 联想到给
联想到给![]() 所在的
所在的![]() 构造全等三角形:过点
构造全等三角形:过点![]() 作
作![]() 轴于点
轴于点![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,通过角度转换可证
,通过角度转换可证![]() ,即有
,即有![]() .设
.设![]() ,
,![]() ,则能用
,则能用![]() 表示
表示![]() 、
、![]() ,利用勾股定理列方程即求出
,利用勾股定理列方程即求出![]() 的值.求得两个
的值.求得两个![]() 的值要分别代入计算讨论合理性.
的值要分别代入计算讨论合理性.
解:(1)当![]() 时,
时,![]() ,解得:
,解得:![]()
![]() ,
,![]()
当![]() 时,
时,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
(2)在![]() 上截取
上截取![]() ,连接
,连接![]()
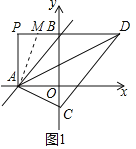
![]() 轴,
轴,![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,
![]() ,即
,即![]()
![]() 矩形
矩形![]() 是正方形
是正方形
![]()
在![]() 与
与![]() 中
中
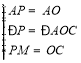
![]()
![]() ,
,![]()
![]()
![]()
![]()
在![]() 与
与![]() 中
中

![]()
![]()
![]()
![]()
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 轴,
轴,![]() 轴
轴
![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,![]()
在![]() 与
与![]() 中,
中,
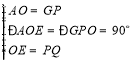
![]()
![]() ,
,![]()
![]()
即![]()
在![]() 与
与![]() 中,
中,

![]()
![]()
设![]() ,则
,则![]()
![]() ,
,![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
解得:![]() ,
,![]()
①当![]() 时,
时,![]() ,
,![]()
![]()
![]()
![]()
![]()
②当![]() 时,
时,![]() ,
,![]()
![]()
![]()
![]()
综上所述,点![]() 坐标为
坐标为![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2![]() ,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )
,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )

A.3B.4C.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() ,
,![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
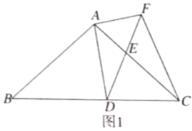
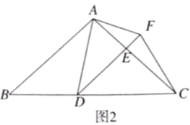
(1)求证:![]() ;
;
(2)当![]() 时(如图2),求
时(如图2),求![]() 的长;
的长;
(3)点![]() 在
在![]() 边上运动的过程中,是否存在某个位置,使得
边上运动的过程中,是否存在某个位置,使得![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
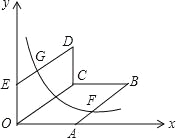
【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=![]() (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
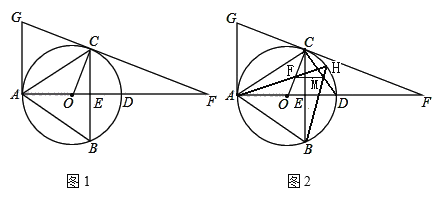
【题目】如图1,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=![]() ,BC=8.
,BC=8.
(1)求证:CF是⊙O的切线;
(2)求⊙O的半径OC;
(3)如图2,⊙O的弦AH经过半径OC的中点F,连结BH交弦CD于点M,连结FM,试求出FM的长和△AOF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
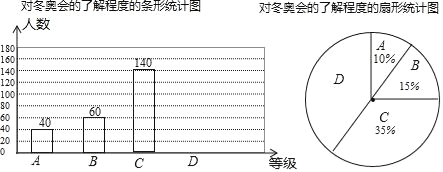
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com