
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() ,
,![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
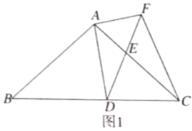
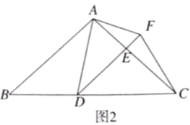
(1)求证:![]() ;
;
(2)当![]() 时(如图2),求
时(如图2),求![]() 的长;
的长;
(3)点![]() 在
在![]() 边上运动的过程中,是否存在某个位置,使得
边上运动的过程中,是否存在某个位置,使得![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]() ;(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.
;(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.
【解析】
(1)利用等腰三角形的性质有∠B=∠ACB,然后根据∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B即可得出∠BAD=∠CDE,则结论可证;
(2)过点A作AM⊥BC于M,设![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△ABD∽△CBA,
中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△ABD∽△CBA,
则![]() ,由此可求出DB的长度,最后再利用平行线分线段成比例有
,由此可求出DB的长度,最后再利用平行线分线段成比例有![]() ,即可求出AE的长度;
,即可求出AE的长度;
(3)作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N,首先证明四边形AMHN为矩形,
则有∠MAN=90°,MH=AN,然后设![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△AFN∽△ADM,
中利用勾股定理求出k的值,然后利用等腰三角形三线合一求出BC的长度,然后证明△AFN∽△ADM,
利用相似三角形的性质可求出AN的长度,进而求出CH的长度,再根据等腰三角形三线合一求出CD的长度,最后利用BD=BC-CD即可得出答案.
(1)证明:∵AB=AC,
∴∠B=∠ACB,
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE,
∴△BAD∽△DCE.
(2)解:过点A作AM⊥BC于M.
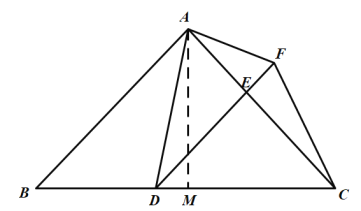
∵![]() ,
,
∴设![]() ,
,
![]()
∴![]()
解得![]() 或
或![]() (舍去)
(舍去)
∵AB=AC,AM⊥BC,
∴BC=2BM=2×4k=16,
∵DE∥AB,
∴∠BAD=∠ADE,
∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() ,
,
∴![]()
![]() ,
,
∵DE∥AB,
∴![]() ,
,
∴![]()
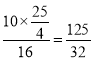 .
.
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
理由:作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N.
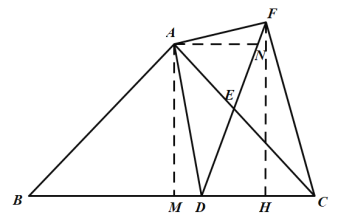
∵FH⊥BC,AM⊥BC,AN⊥FH,
∴∠NHM=∠AMH=∠ANH=90°,
∴四边形AMHN为矩形,
∴∠MAN=90°,MH=AN,
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD,
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM,
∴![]() ,
,
∴![]() ,
,
∴CH=CM-MH=CM-AN=8-![]() =
=![]() ,
,
当DF=CF时,由点D不与点C重合,可知△DFC为等腰三角形,
∵FH⊥DC,
∴CD=2CH=7,
∴BD=BC-CD=16-7=9,
∴点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.


科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
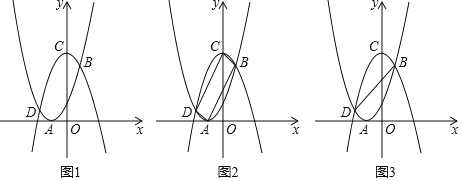
【题目】如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移5个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点C,两函数图象分别交于B、D两点.
(1)求函数y=ax2+bx+c的解析式;
(2)如图2,连接AD、CD、BC、AB,判断四边形ABCD的形状,并说明理由.
(3)如图3,连接BD,点M是y轴上的动点,在平面内是否存在一点N,使以B、D、M、N为顶点的四边形为矩形?若存在,请求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
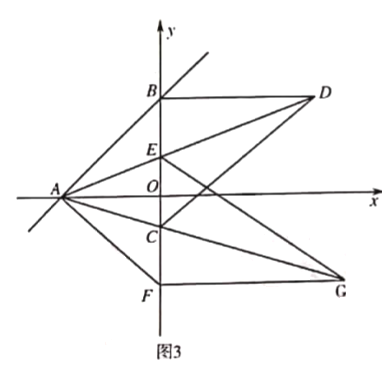
【题目】已知点![]() 是平行四边形
是平行四边形![]() 的边
的边![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
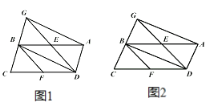
(1)如图1,求证:![]() ;
;
(2)如图2,当四边形![]() 是矩形时,请你确定四边形
是矩形时,请你确定四边形![]() 的形状并说明.
的形状并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在以“青春心向觉,建功新时代”为主题的校园文化艺术节期间,举办了![]() 合唱,
合唱,![]() 群舞,
群舞,![]() 书法,
书法,![]() 演讲共四个项目的比赛,要求每位学生必须参加且仅参加一项,小红随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
演讲共四个项目的比赛,要求每位学生必须参加且仅参加一项,小红随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
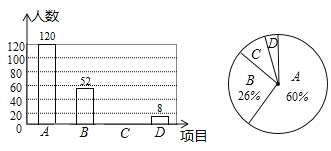
(1)本次调查的学生总人数是多少?扇形统计图中“![]() ”部分的圆心角度数是多少?
”部分的圆心角度数是多少?
(2)请将条形统计图补充完整;
(3)若全校共有1800名学生,请估计该校报名参加书法和演讲比赛的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 交
交![]() 轴负半轴)轴正半轴于
轴负半轴)轴正半轴于![]() 两点,
两点, ![]() 的面积为4.5;
的面积为4.5;
![]() 如图1.求
如图1.求![]() 的值;
的值;
![]() 如图2.在
如图2.在![]() 轴负半轴上取点
轴负半轴上取点![]() .点
.点![]() 在第一象限,
在第一象限,![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如图3,在
如图3,在![]() 的条件下.
的条件下.![]() 交
交![]() 轴于点
轴于点![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
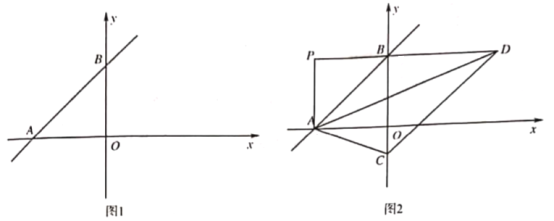
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
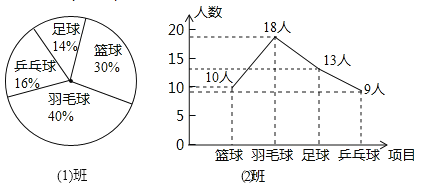
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com