
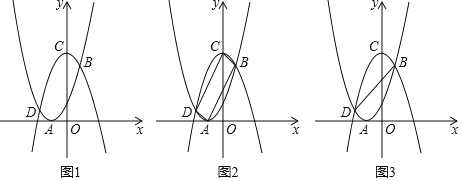
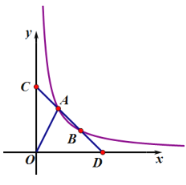
����Ŀ����ͼ��ʾ�������κ���y=x2+2x+1��ͼ����x�ᷭ�ۣ�Ȼ������ƽ��1����λ��������ƽ��5����λ���õ����κ���y=ax2+bx+c��ͼ����y=x2+2x+1��ͼ��Ķ���Ϊ��A������y=ax2+bx+c��ͼ��Ķ���Ϊ��C��������ͼ��ֱ���B��D���㣮
��1������y=ax2+bx+c�Ľ���ʽ��
��2����ͼ2������AD��CD��BC��AB���ж��ı���ABCD����״����˵�����ɣ�
��3����ͼ3������BD����M��y���ϵĶ��㣬��ƽ�����Ƿ����һ��N��ʹ��B��D��M��NΪ������ı���Ϊ���Σ������ڣ������N������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2+5����2���ı���ABCD��ƽ���ı��Σ����ɼ���������3�����ڣ���N����Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��2)��(��3��2)��
)��(3��2)��(��3��2)��
��������
(1)����Գƺ�ƽ�Ƶ����ʿ���⣻
(2)�ֱ������A����B����C����D���꣬��������빫ʽ����AB��CD��AD��BC��AC��BD�ij���������Ա���ȵ��ı�����ƽ���ı��ο�֤�ı���ABCD��ƽ���ı��Σ�
(3)������������ۣ����þ��ε����ʣ�����⣮
(1)��y=x2+2x+1=(x+1)2���ҽ����κ���y=x2+2x+1��ͼ����x�ᷭ�ۣ�Ȼ������ƽ��1����λ��������ƽ��5����λ��
��y=��(x+1��1)2+5=��x2+5��
(2)�ı���ABCD��ƽ���ı��Σ��������£�
��y=��x2+5�Ķ���Ϊ��C��
���C������Ϊ(0��5)��
�ߺ���y=x2+2x+1��ͼ��Ķ���Ϊ��A��
���A(��1��0)��
����������ɵã� ��
��
�� ![]() ��
�� ![]() ��
��
���D������Ϊ(��2��1)����B������Ϊ(1��4)��
�ߵ�D(��2��1)����B(1��4)����A(��1��0)����C(0��5)��
��![]() ��
��
ͬ������ã�CD=![]() ��AD=
��AD=![]() ��BC=
��BC=![]() ��AC=
��AC=![]() ��BD=3
��BD=3![]() ��
��
��AB=CD��AD=BC��
���ı���ABCD��ƽ���ı��Σ�
(3)���ڣ�
���N(x��y)
��BDΪ���εıߣ��ı���BDMN�Ǿ���ʱ��

�ߵ�D������Ϊ(��2��1)����B������Ϊ(1��4)��
��ֱ��BD����ʽΪ��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��ֱ��BD����ʽΪ��y=x+3��
��DM��BD��
����ֱ��DM�Ľ���ʽΪ![]() ��
��
����D������Ϊ(��2��1)����ã�![]() ��
��
��ã�![]() ��
��
��ֱ��DM�Ľ���ʽΪy=��x��1��
���M������Ϊ(0����1)��
��BM��DN����ƽ�֣�
��![]() ��
��![]() ��
��
��x=3��y=2��
���N������Ϊ(3��2)��
��BDΪ���εıߣ��ı���BDNM�Ǿ���ʱ��

�ߵ�D������Ϊ(��2��1)����B������Ϊ(1��4)��ֱ��BD����ʽΪ��y=x+3��
��BM��BD��
����ֱ��BM�Ľ���ʽΪ![]() ��
��
����B������Ϊ(1��4)����ã�![]() ��
��
��ã�![]() ��
��
��ֱ��BM�Ľ���ʽΪy=��x+5��
���M������Ϊ(0��5)��
��BN��DM����ƽ�֣�
��![]() ��
��![]() ��
��
��x=��3��y=2��
���N������Ϊ(��3��2)��
��BDΪ�Խ��ߣ�
�ߵ�D��B��N������ֱ�Ϊ(��2��1)�� (1��4)�� (x��y)��
��M�ĺ�����Ϊ0�����M��������Ϊ![]() ��
��

��BD��MN����ƽ�֣�
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��N������Ϊ(![]() ��
��![]() )����M������Ϊ(0��5��y)��
)����M������Ϊ(0��5��y)��
��BD=MN��
��![]()
�����ã�![]()
��ã�![]() ��
��
���N������Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
������������N����Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��2)��(��3��2)��
)��(3��2)��(��3��2)��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Խ�ͨ������˽������ȫУ��������˲���ѧ������������Ϊ���֣�![]() ���dz��˽⣬
���dz��˽⣬![]() ���Ƚ��˽⣬
���Ƚ��˽⣬![]() �������˽⣬
�������˽⣬![]() ����̫�˽⣬�����˴ε������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
����̫�˽⣬�����˴ε������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
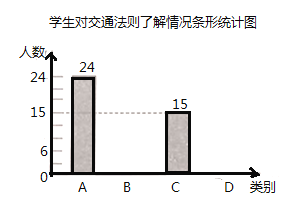
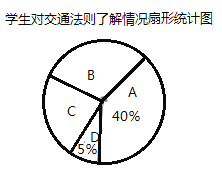
��1�����ι�����_______��ѧ��������ͳ��ͼ��![]() ����Ӧ���ε�Բ�ĽǶ�����_______��
����Ӧ���ε�Բ�ĽǶ�����_______��
��2����ȫ����ͳ��ͼ��
��3��ѧУ���Ӽס��ҡ���������λѧ���������ȡ����ѧ���μ�������ͨ���澺���������б�����״ͼ�ķ������������ѧ��ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶10�����300��ѧ�������μ�ѧУ���е��о����л��ѧУ�������4������⣺A����ˮ��ϼ��ò���죻B��ƽ������֪ʶ���죻C��ɽ�غ�ɫ�Ļ����죻D����������˾�Ļ����죬Ϊ�˽�ѧ��ϲ���Ļ���⣬ѧ���Ὺչ��һ�ε����о����뽫����Ĺ��̲�ȫ
��1���ռ����ݣ�ѧ����ƻ�����ѧ��ϲ���Ļ��������������������Ķ���ѡ���������______��������ţ�
��ѡ�����꼶3�ࡢ4�ࡢ5��ѧ����Ϊ�������
��ѡ��ѧУ������Ӱ���ŵ�ѧ����Ϊ�������
��ѡ�����ѧ��Ϊ6�ı�����ѧ����Ϊ�������
��2���������������ݣ�ͨ�����˺�ѧ����ͬѧ����������������������ͳ��ͼ�����ͳ��ͼ��������
ijУ���꼶ѧ��ϲ���Ļ��������ͳ��ͼijУ���꼶ѧ��ϲ���Ļ��������ͳ��ͼ
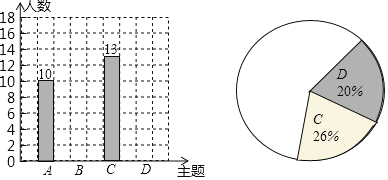
��3���������ݡ��ƶϽ��ۣ��������������������ѧУ�Ƽ����λ�����⣬����Ƽ���______����A-D����ĸ���ţ�������ȫ�꼶��Լ�ж�����ѧ��ϲ���������
��4������5��ѧ����ɲ���3��2Ů���У����ѡȡ2��ͬѧ���λ���鳤���鳤������������ͬѧǡ����1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ������
������![]() ��
��
��1�����������Ľ���ʽ��
��2����![]() ��
��![]() ����������ϣ���
����������ϣ���![]() ��
��![]() ����������ϣ�ֱ��
����������ϣ�ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ������������ͼ������һ��
������������ͼ������һ��![]() ����
����![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����5��0������OAΪ�뾶����Բ����C�ǵ�һ������Բ����һ���㣬����AC��BC�����ӳ�BC����D��ʹCD��BC������D��x�ᴹ�ߣ��ֱ�x�ᡢֱ��AC�ڵ�E��F����EΪ���㣬����OF��

��1������BAC��30ʱ������ABC�������
��2����DE��8ʱ�����߶�EF�ij���
��3���ڵ�C�˶������У��Ƿ�����Ե�E��O��FΪ���������������ABC���ƣ������ڣ��������E�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���ϵĶ��㣨��
���ϵĶ��㣨��![]() �����
�����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ������
������![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
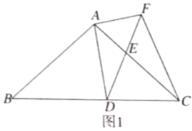
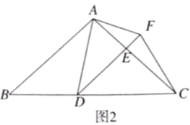
��1����֤��![]() ��
��
��2����![]() ʱ����ͼ2������
ʱ����ͼ2������![]() �ij���
�ij���
��3����![]() ��
��![]() �����˶��Ĺ����У��Ƿ����ij��λ�ã�ʹ��
�����˶��Ĺ����У��Ƿ����ij��λ�ã�ʹ��![]() �������ڣ������ʱ
�������ڣ������ʱ![]() �ij����������ڣ���˵�����ɣ�
�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ڽ���Բ
�ڽ���Բ![]() ����
����![]() ��
Ϊ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
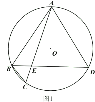 ����������
����������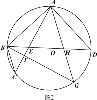 ����������
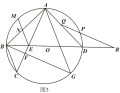
����������
��1����ͼ1����֤����![]() ��
��![]() ��
��
��2����ͼ2����![]() ��
��![]() �ڵ�
�ڵ�![]() ����Բ
����Բ![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �Ķ�����
�Ķ�����
��3����ͼ3���ڣ�2���������£�Բ![]() ��һ��
��һ��![]() ���
���![]() ����
����![]() �Գƣ�����
�Գƣ�����![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
Ϊ��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() ��
��![]() ���ܳ�Ϊ20��
���ܳ�Ϊ20��![]() ����Բ
����Բ![]() �뾶��
�뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�ڽ��ڡ�O��ֱ��AD��BC�ڵ�E���ӳ�AD����F��ʹDF��2OD������FC���ӳ�������A�������ڵ�G��������AG��BC������OC����cos��BAC��![]() ��BC��8��
��BC��8��
��1����֤��CF�ǡ�O�����ߣ�
��2�����O�İ뾶OC��
��3����ͼ2����O����AH�����뾶OC���е�F������BH����CD�ڵ�M������FM�������FM�ij�����AOF�������
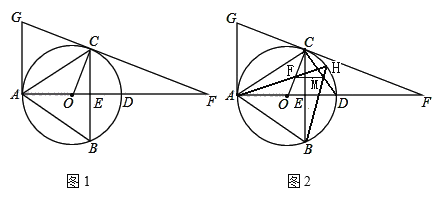
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() �ı�
�ı�![]() ��
��![]() ���ϣ���
���ϣ���![]() ������Ϊ
������Ϊ![]() ����
����![]() �ǶԽ���
�ǶԽ���![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ��
��![]() ���ϣ���
���ϣ���![]() ���ʱ����
���ʱ����![]() ������Ϊ______.
������Ϊ______.
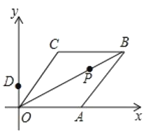
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com