
【题目】某校对交通法则的了解情况在全校随机调查了部分学生,调查结果分为四种:![]() .非常了解,
.非常了解,![]() .比较了解,
.比较了解,![]() .基本了解,
.基本了解,![]() .不太了解,并将此次调查结果整理绘制成下面不完整的条形统计图和扇形统计图.
.不太了解,并将此次调查结果整理绘制成下面不完整的条形统计图和扇形统计图.
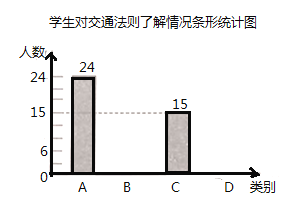
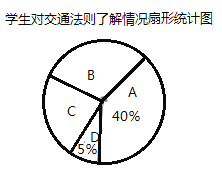
(1)本次共调查_______名学生;扇形统计图中![]() 所对应扇形的圆心角度数是_______;
所对应扇形的圆心角度数是_______;
(2)补全条形统计图;
(3)学校准备从甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求甲和乙两名学生同时被选中的概率.
【答案】(1)60,90°;(2)补图见解析;(3)![]() .
.
【解析】
(1)用A类的人数除以它所占的百分比得到调查的总人数,然后用C类人数所占的百分比乘以360°得到扇形统计图中C所对应扇形的圆心角度数;
(2)分别计算出D类、B类的人数,然后补全条形统计图;
(3)画树状图展示所有12种等可能的结果数,找出甲和乙两名学生同时被选中的结果数,然后利用概率公式求解.
(1)![]() ,所以本次调查了60名学生;
,所以本次调查了60名学生;
扇形统计图中![]() 所对应扇形的圆心角度数
所对应扇形的圆心角度数![]() ;
;
故答案为:60,90°;
(2)![]() 类学生数为
类学生数为![]() (名),
(名),![]() 类学生数为
类学生数为![]() (名),补全条形统计图为:
(名),补全条形统计图为:
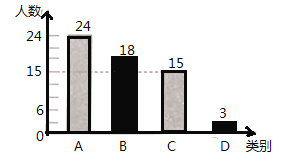
(3)画树状图为:
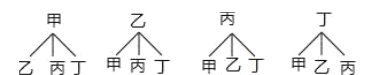
共有12种等可能的结果数,其中甲和乙两名学生同时被选中的结果数为2,所以甲和乙两名学生同时被选中的概率![]() .
.


科目:初中数学 来源: 题型:
【题目】给定一个函数,如果这个函数的图象上存在一个点,它的横、纵坐标相等,那么这个点叫做该函数的不变点.
(1)一次函数![]() 的不变点的坐标为______.
的不变点的坐标为______.
(2)二次函数![]() 的两个不变点分别为点
的两个不变点分别为点![]() (
(![]() 在
在![]() 的左侧),将点
的左侧),将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)已知二次函数![]() 的两个不变点的坐标为
的两个不变点的坐标为![]() .
.
①求![]() 的值;
的值;
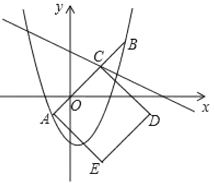
②如图,设抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .点
.点![]() 为一次函数
为一次函数![]() 的不变点,以线段
的不变点,以线段![]() 为边向下作正方形
为边向下作正方形![]() .当
.当![]() 两点中只有一个点在封闭图形
两点中只有一个点在封闭图形![]() 的内部(不包含边界)时,求出
的内部(不包含边界)时,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内,![]() .
.
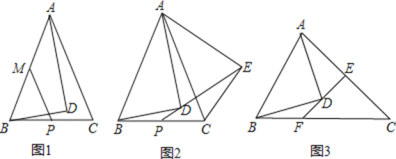
(1)如图1,若![]() ,
,![]() ,
,![]() ,点,
,点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 递时针旋转一定角度,得到
递时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长变
并延长变![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,若![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 、
、![]() 、
、![]() 之间的关系(不需要证明).
之间的关系(不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
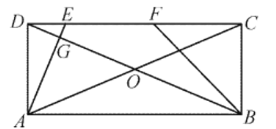
【题目】如图,矩形![]() 的对角线交于点
的对角线交于点![]() .点
.点![]() 在
在![]() 边上,
边上,![]() 连结
连结![]() 交对角线
交对角线![]() 于点
于点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .
.
(1)求证:![]() .
.
(2)判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)若![]() 和
和![]() 面积分别为
面积分别为![]() 和
和![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在去年的体育中考中,某校6名学生的体育成绩统计如下表:
成绩 | 17 | 18 | 20 |
人数 | 2 | 3 | 1 |
则下列关于这组数据的说法错误的是( )
A.众数是18B.中位数是18C.平均数是18D.方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵![]() 元,用
元,用![]() 元购进乙书包的个数与用
元购进乙书包的个数与用![]() 元购进甲书包的个数相等.
元购进甲书包的个数相等.
(1)求甲、乙两种书包的进价分别为多少元?
(2)商户购进甲、乙两种书包共![]() 个进行试销,其中甲书包的个数不少于
个进行试销,其中甲书包的个数不少于![]() 个,且甲书包的个数 的
个,且甲书包的个数 的![]() 倍不大于乙书包的个数,已知甲书包的售价为
倍不大于乙书包的个数,已知甲书包的售价为![]() 元/个,乙书包的售价为
元/个,乙书包的售价为![]() 元/个,且 全部售出,设购进甲书包
元/个,且 全部售出,设购进甲书包![]() 个,求该商店销售这批书包的利润
个,求该商店销售这批书包的利润![]() 与
与![]() 之间的函数关系式,并 写出
之间的函数关系式,并 写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,该店将![]() 个书包全部售出后,使用所获的利润又购进
个书包全部售出后,使用所获的利润又购进![]() 个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利
个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利![]() 元.请求出该店第二次进货所选用的进货方案?
元.请求出该店第二次进货所选用的进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() .
.
(1)若点![]() 也在该抛物线上,请用含
也在该抛物线上,请用含![]() 的关系式表示
的关系式表示![]() ;
;
(2)若该抛物线上任意不同两点![]() 、
、![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;若以原点
;若以原点![]() 为圆心,
为圆心,![]() 为半径的圆与抛物线的另两个交点为
为半径的圆与抛物线的另两个交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),且
左侧),且![]() 有一个内角为
有一个内角为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)在(2)的条件下,若点![]() 与点
与点![]() 关于点
关于点![]() 对称,且
对称,且![]() 、
、![]() 、
、![]() 三点共线,求证:
三点共线,求证:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
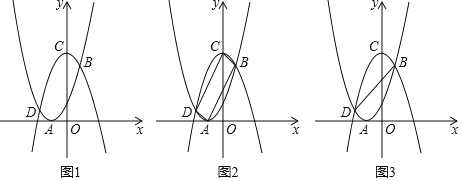
【题目】如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移5个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点C,两函数图象分别交于B、D两点.
(1)求函数y=ax2+bx+c的解析式;
(2)如图2,连接AD、CD、BC、AB,判断四边形ABCD的形状,并说明理由.
(3)如图3,连接BD,点M是y轴上的动点,在平面内是否存在一点N,使以B、D、M、N为顶点的四边形为矩形?若存在,请求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com