
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() ,过点
,过点![]() 作
作![]() ,与
,与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() ,与边
,与边![]() 相交于点
相交于点![]() ,与对角线
,与对角线![]() 相交于点
相交于点![]() .若
.若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
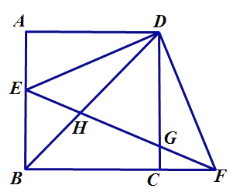
在正方形ABCD中,由FD与DE垂直,利用等式的性质得到一对角相等,再由一对直角相等,且AD=DC,利用AAS得到三角形DAE与三角形DCF全等,利用全等三角形对应边相等得到AE=CF,进而求出BE的长
∵在正方形ABCD中,∠BCD=90°,BC=CD=6,
∴BD=6![]() .
.
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
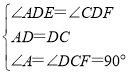 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF.
又∵BD=BF=6![]() ,
,
∴AE=CF=BF-BC=6![]() -6,
-6,
∴BE=AB-AE=6-(6![]() -6)=12-6
-6)=12-6![]() ,
,
即BE的长为12-6![]() ;
;
故选:C.


科目:初中数学 来源: 题型:
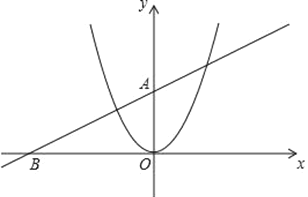
【题目】已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.
(1)求直线的解析式;
(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;
(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数学理解:如图①,![]() 是等腰直角三角形,过斜边
是等腰直角三角形,过斜边![]() 的中点
的中点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
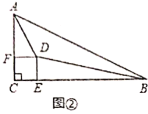
(2)问题解决:如图②,在任意直角![]() 内,找一点
内,找一点![]() ,过点
,过点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
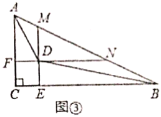
(3)联系拓广;如图③,在(2)的条件下,分别延长![]() ,
,![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
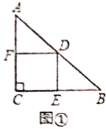
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对交通法则的了解情况在全校随机调查了部分学生,调查结果分为四种:![]() .非常了解,
.非常了解,![]() .比较了解,
.比较了解,![]() .基本了解,
.基本了解,![]() .不太了解,并将此次调查结果整理绘制成下面不完整的条形统计图和扇形统计图.
.不太了解,并将此次调查结果整理绘制成下面不完整的条形统计图和扇形统计图.
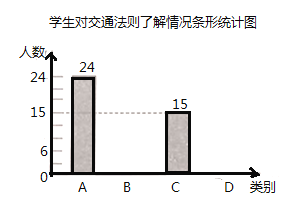
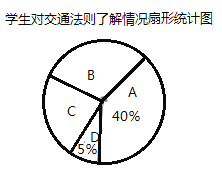
(1)本次共调查_______名学生;扇形统计图中![]() 所对应扇形的圆心角度数是_______;
所对应扇形的圆心角度数是_______;
(2)补全条形统计图;
(3)学校准备从甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求甲和乙两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距![]() 车和
车和![]() 车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地
车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地![]() 后,
后,![]() 车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比
车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比![]() 车晚
车晚![]() 到达目的地.两车的速度始终保持不变,如图是
到达目的地.两车的速度始终保持不变,如图是![]() 两车距各自出 发地的路程
两车距各自出 发地的路程![]() (单位:
(单位:![]() ),
),![]() (单位:
(单位:![]() )与
)与![]() 车出发时间
车出发时间![]() (单位:
(单位:![]() )的函数图象,请结合图象信息解答下列问题:
)的函数图象,请结合图象信息解答下列问题:

(1)A车的速度为 ![]() 车的速度为
车的速度为
(2)求甲、丙两地的距离;
(3)求![]() 车出发多长时间,两车相距
车出发多长时间,两车相距![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
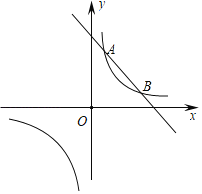
【题目】已知一次函数y=﹣x+m的图象与反比例函数![]() 的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2![]() ,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )
,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )

A.3B.4C.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
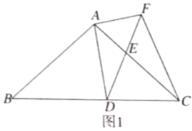
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() ,
,![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
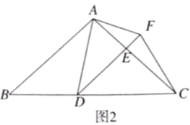
(2)当![]() 时(如图2),求
时(如图2),求![]() 的长;
的长;
(3)点![]() 在
在![]() 边上运动的过程中,是否存在某个位置,使得
边上运动的过程中,是否存在某个位置,使得![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com