
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

【答案】![]() 或
或![]()
【解析】依据△DCM为直角三角形,需要分两种情况进行讨论:当∠CDM=90°时,△CDM是直角三角形;当∠CMD=90°时,△CDM是直角三角形,分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到折痕MN的长.
分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
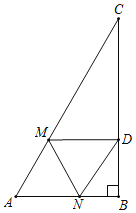
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,
+4,
∴∠C=30°,AB=![]() AC=
AC=![]() +2,
+2,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=![]() DN=
DN=![]() AN,
AN,
∴BN=![]() AB=
AB=![]() ,
,
∴AN=2BN=![]() ,
,
∵∠DNB=60°,
∴∠ANM=∠DNM=60°,
∴∠AMN=60°,
∴AN=MN=![]() ;
;
②如图,当∠CMD=90°时,△CDM是直角三角形,
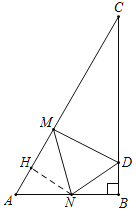
由题可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=![]() DN=
DN=![]() AN,BN=
AN,BN=![]() BD,
BD,
又∵AB=![]() +2,
+2,
∴AN=2,BN=![]() ,
,
过N作NH⊥AM于H,则∠ANH=30°,
∴AH=![]() AN=1,HN=
AN=1,HN=![]() ,
,
由折叠可得,∠AMN=∠DMN=45°,
∴△MNH是等腰直角三角形,
∴HM=HN=![]() ,
,
∴MN=![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() ,一只小虫从点
,一只小虫从点![]() 出发沿着数轴的正方向以每秒
出发沿着数轴的正方向以每秒![]() 个单位的速度爬行至
个单位的速度爬行至![]() 点,又立即返回到
点,又立即返回到![]() 点,共用了
点,共用了![]() 秒钟.
秒钟.
![]() 点
点![]() 对应的数是_.
对应的数是_.
![]() 若小虫返回到
若小虫返回到![]() 点后再作如下运动:第一次向右爬行
点后再作如下运动:第一次向右爬行![]() 个单位,第
个单位,第![]() 次向左爬行
次向左爬行![]() 个单位,第三次向右爬行
个单位,第三次向右爬行![]() 个单位,第四次向左爬行
个单位,第四次向左爬行![]() 个单位,..依此规律爬下去, 它第
个单位,..依此规律爬下去, 它第![]() 次爬行所停的点所对应的数是 .
次爬行所停的点所对应的数是 .
第![]() 次爬行所停的点所对应的数是
次爬行所停的点所对应的数是
![]() 在
在![]() 的条件下,求小虫第
的条件下,求小虫第![]() 次爬行所停的点所对应的数.
次爬行所停的点所对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=∠COD=90°.
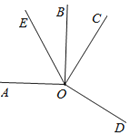
(1)猜想:∠BOC与∠AOD之间的数量关系,并说明理由;
(2)若OE平分∠AOC,∠BOC=34°,求∠AOE的余角的度数;
(3)若OC表示北偏东34°方向,在(2)的条件下直接写出OE表示的方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数学家莫伦发现了世界上第一个完美长方形,它恰好能够分割成大小不同的正方形,请你完成下面计算.
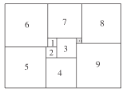
(1)如果标注1,2的正方形的边长分别是1和1.2,那么标注3的正方形的边长为________.标注5的正方形的边长为________.
(2)如果标注1,2的正方形的边长分别是![]() 和
和![]() ,求标注10的正方形的边长是多少?(用含
,求标注10的正方形的边长是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若在(2)的条件下,“勤奋小组”继续探究发现,标注9的正方形边长有两种表示方法,若标注9的正方形的边长是15,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
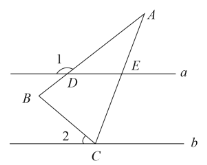
A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
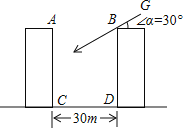
【题目】两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.
(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?
(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.
(1)当k=2时,直线l1、l2与x轴围成的三角形的面积S2=______;
(2)当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2,S3,S4,……,S2018,则S2+S3+S4+……+S2018=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2.求证:∠3 +∠4=180°.
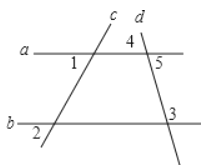
证明:∵∠1=∠2(已知)
∴ a∥b( )
∴∠3 +∠5=180° (两直线平行,同旁内角互补)
又 ∵∠4=∠5 ( )
∴∠3 +∠4=180° (等量代换)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com