
【题目】如图,已知∠AOB=∠COD=90°.
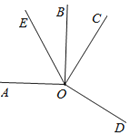
(1)猜想:∠BOC与∠AOD之间的数量关系,并说明理由;
(2)若OE平分∠AOC,∠BOC=34°,求∠AOE的余角的度数;
(3)若OC表示北偏东34°方向,在(2)的条件下直接写出OE表示的方向.
【答案】(1)∠BOC+∠AOD=180°,理由见解析;(2)28°;(3)OE表示的方向为北偏西28°
【解析】
(1)首先根据图形可知∠AOB+∠BOC+∠COD+∠AOD=360°,据此进一步用它们四个角的和减去∠AOB与∠COD即可得出答案;
(2)首先根据题意求出∠AOC的度数,然后利用角平分线性质得出∠AOE的度数,最后进一步计算出它的余角即可;
(3)根据题意可求出∠BOE度数,然后参照OC表示北偏东34°方向即可得出OE表示的方向.
(1)∠BOC与∠AOD之间的数量关系为:∠BOC+∠AOD=180°,
理由如下:
∵∠AOB=∠COD=90°,∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠BOC+∠AOD=360°∠AOB∠COD=180°;
(2)∵∠AOB=90°,∠BOC=34°,
∴∠AOC=∠AOB+∠BOC=124°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=62°,
∠AOC=62°,
∴90°62°=28°,
即∠AOE的余角为28°;
(3)由(2)可得:∠AOE =62°,
∵∠AOB =90°,
∴∠BOE=90°62=28°,
∵OC表示北偏东34°方向,
∴OE表示的方向为北偏西28°.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
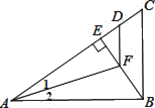
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积=![]() (上底+下底)×高)
(上底+下底)×高)
公式的探究与应用:
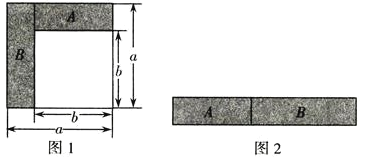
(1)如图1所示,可以求出阴影部分的面积是 ;
(2)若将图1的阴影部分裁剪下来,重新拼成一个如图2所示的长方形,求此长方形的面积.
(3)比较两图阴影部分的面积,可以得到一个公式:
;
(4)运用公式计算
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车行去年A型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少20%.
(1)求今年A型车每辆车的售价.
(2)该车行计划新进一批A型车和B型车共45辆,已知A、B型车的进货价格分别是1100元,1400元,今年B型车的销售价格是2000元,要求B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数是
表示的数是![]() 若动点
若动点![]() 从原点
从原点![]() 出发,以
出发,以![]() 个单位/秒的速度向左运动;同时另一动点
个单位/秒的速度向左运动;同时另一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为
个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为![]() (秒).
(秒).
![]()
![]() 当
当![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离;
的距离;
![]() 当
当![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离;
的距离;
![]() 当点
当点![]() 到原点
到原点![]() 的距离为
的距离为![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
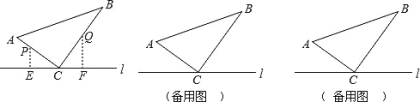
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
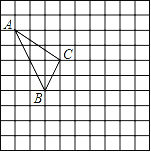
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张相同的卡片,分别写有数字![]() 2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
(1)从中任意抽出一张,抽到卡片上的数字为负数的概率;
(2)从中任意抽出两张,用树状图或表格列出所有可能的结果,并求抽出卡片上的数字积为正数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com