【题目】如图，在数轴上点
表示的数是
若动点
从原点
出发，以
个单位/秒的速度向左运动；同时另一动点
从点出发，以
个单位/秒的速度也向左运动，到达原点后立即以原来的速度返回，向右运动，设运动的时间为
(秒)．
当
时，求点到原点的距离；
当
时，求点到原点的距离；
当点到原点的距离为时，求点到原点的距离．
初中学业考试导与练系列答案科目：初中数学 来源： 题型：
【题目】如图，∠CAB=∠DBA，再添加一个条件，不一定能判定△ABC≌△BAD的是（ ）
A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解学生的课外阅读情况，对部分学生进行了调查，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制如下两幅不完整的统计图．
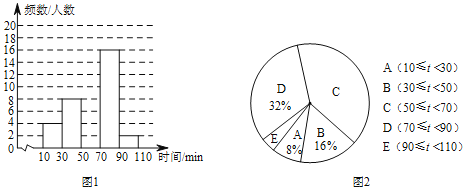
请你根据以上信息解答下列问题：
（1）本次调查活动采取了 调查方式，样本容量是 ．
（2）图2中C的圆心角度数为 度，补全图1的频数分布直方图．
（3）该校有900名学生，估计该校学生平均每天的课外阅读时间不少于50min的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为边作△CDE，其中CD=CE，∠DCE=90°，连接BE．
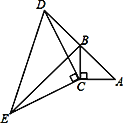
(1)求证：△ACD≌△BCE.
(2)若AB=6cm，则BE=______cm．
(3)BE与AD有何位置关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠AOB=∠COD=90°．
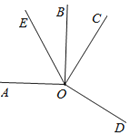
（1）猜想：∠BOC与∠AOD之间的数量关系，并说明理由；
（2）若OE平分∠AOC，∠BOC=34°，求∠AOE的余角的度数；
（3）若OC表示北偏东34°方向，在（2）的条件下直接写出OE表示的方向．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90°，分别以点A和点B为圆心，以相同的长（大于
AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E．若AC＝3，AB＝5，则DE等于（ ）
A. 2 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠A=30°，直线a∥b，顶点C在直线b上，直线a交AB于点D，交AC于点E，若∠1=145°，则∠2的度数是( )
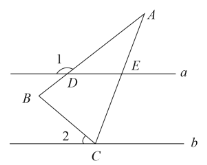
A.30°B.35°C.40°D.45°
查看答案和解析>>
科目：初中数学 来源： 题型：
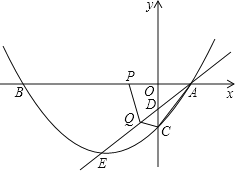
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C（0，﹣
），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=
．
（1）求抛物线的解析式；
（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动时间为t秒．
①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．
②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
