
【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )

A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=90°.
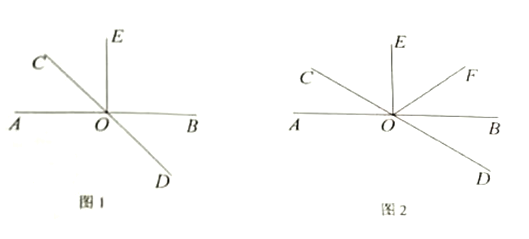
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
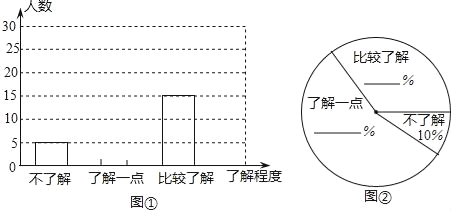
(3)在扇形统计图中,“比较了解”所在扇形的圆心角的度数是 .
(4)请你估计该校七年级约有 名学生比较了解“低碳”知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
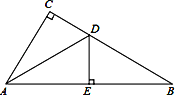
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
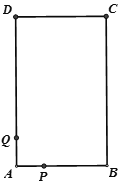
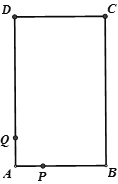
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,B、C分别是∠PAQ的两边AP,AQ上的点,直线l垂直平分BC。

(1)尺规作图:在直线1上求作一点O,使得点O到AP、AQ距离相等(不写作法,保留作图痕迹);
(2)过O点作OE⊥AP,OF⊥AQ,垂足分别为E、F。求证BE=CF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com