
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作△CDE,其中CD=CE,∠DCE=90°,连接BE.
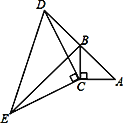
(1)求证:△ACD≌△BCE.
(2)若AB=6cm,则BE=______cm.
(3)BE与AD有何位置关系?请说明理由.
【答案】(1)证明见解析;(2)12;(3)垂直平分.
【解析】
(1)根据等腰直角三角形的性质得到CD=CE,CA=CB,然后利用“SAS”可判断△ACD≌△BCE即可;
(2)根据全等三角形的性质得到AD=BE即可;
(3)由全等三角形的性质得出∠EBC=∠A,由△ABC是等腰直角三角形,则∠A=∠ABC=∠EBC=45°,则BE⊥AD,即可得到答案.
解:(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS);
(2)解:∵DB=AB,
∴AD=2AB=12cm,
由(1)得:△ACD≌△BCE,
∴BE=AD=12cm;
故答案为:12;
(3)由△ACD≌△BCE,
∴∠EBC=∠A,
∵△ABC是等腰直角三角形,
∴∠A=∠ABC=∠EBC=45°,
∴∠ABE=90°,
即BE⊥AD.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人.行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
5 | 2 | -4 | -3 | 10 |
(1)接送完第5批客人后,该驾驶员在公司 边(填南或北),距离公司 千米.
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油 升.
(3)若该出租车的计价标准为:行驶路程不超过3![]() 收费10元,超过3
收费10元,超过3![]() 的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
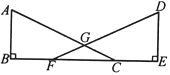
【题目】如图,点B,F,C,E在同一直线上,AC,DF相交于点G,且△ABC≌△DEF
(1)若△ABC的周长为12cm,AB=3cm,BC=4cm,求DF的长.
(2)若DE⊥BC与点E,∠A=65°,求∠AGF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数是
表示的数是![]() 若动点
若动点![]() 从原点
从原点![]() 出发,以
出发,以![]() 个单位/秒的速度向左运动;同时另一动点
个单位/秒的速度向左运动;同时另一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为
个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为![]() (秒).
(秒).
![]()
![]() 当
当![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离;
的距离;
![]() 当
当![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离;
的距离;
![]() 当点
当点![]() 到原点
到原点![]() 的距离为
的距离为![]() 时,求点
时,求点![]() 到原点
到原点![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个边长为2![]() ,面积为6的等腰三角形.
,面积为6的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
(k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
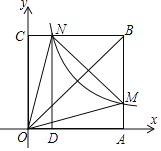
A. △ONC≌△OAM
B. 四边形DAMN与△OMN面积相等
C. ON=MN
D. 若∠MON=45°,MN=2,则点C的坐标为(0,![]() +1)
+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com