【题目】有四张相同的卡片，分别写有数字
2，0，1，5，将它们背面朝上（背面无差别）洗匀后放在桌上．
（1）从中任意抽出一张，抽到卡片上的数字为负数的概率；
（2）从中任意抽出两张，用树状图或表格列出所有可能的结果，并求抽出卡片上的数字积为正数的概率．
状元坊全程突破导练测系列答案科目：初中数学 来源： 题型：
【题目】如图，已知∠AOB=∠COD=90°．
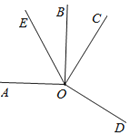
（1）猜想：∠BOC与∠AOD之间的数量关系，并说明理由；
（2）若OE平分∠AOC，∠BOC=34°，求∠AOE的余角的度数；
（3）若OC表示北偏东34°方向，在（2）的条件下直接写出OE表示的方向．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l1：y=（k﹣1）x+k+1和直线l2：y=kx+k+2，其中k为不小于2的自然数．
（1）当k=2时，直线l1、l2与x轴围成的三角形的面积S2=______；
（2）当k=2、3、4，……，2018时，设直线l1、l2与x轴围成的三角形的面积分别为S2，S3，S4，……，S2018，则S2+S3+S4+……+S2018=______．
查看答案和解析>>
科目：初中数学 来源： 题型：
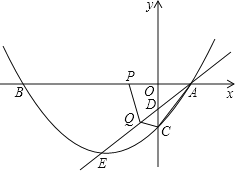
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C（0，﹣
），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=
．
（1）求抛物线的解析式；
（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动时间为t秒．
①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．
②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．
（1）求证：四边形BCED是平行四边形；
（2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
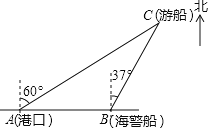
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，
（1）求点C到直线AB的距离；
（2）求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，∠1=∠2．求证：∠3 +∠4=180°．
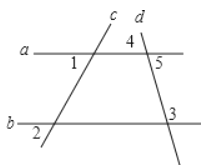
证明：∵∠1=∠2（已知）
∴ a∥b（ ）
∴∠3 +∠5=180° （两直线平行，同旁内角互补）
又 ∵∠4=∠5 （ ）
∴∠3 +∠4=180° （等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
材料一：对于一个两位数
，交换它的个位和十位数字得到的新数
叫这个两位数的“倒序数”.如：23的倒序数是32，50的倒序数是05.
材料二：对于一个两位数，若它的个位数字与十位数字的和小于等于9，则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数的“凸数”.如23的凸数是253.
（1）请求出42的“倒序数”与“凸数”；38有“凸数”吗？为什么？
（2）若一个两位数与它的“倒序数”的和的4倍比这个两位数的“凸数”小132，请求出这个两位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
