
【题目】阅读理解:
材料一:对于一个两位数![]() ,交换它的个位和十位数字得到的新数
,交换它的个位和十位数字得到的新数![]() 叫这个两位数
叫这个两位数![]() 的“倒序数”.如:23的倒序数是32,50的倒序数是05.
的“倒序数”.如:23的倒序数是32,50的倒序数是05.
材料二:对于一个两位数![]() ,若它的个位数字与十位数字的和小于等于9,则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数
,若它的个位数字与十位数字的和小于等于9,则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数![]() 的“凸数”.如23的凸数是253.
的“凸数”.如23的凸数是253.
(1)请求出42的“倒序数”与“凸数”;38有“凸数”吗?为什么?
(2)若一个两位数与它的“倒序数”的和的4倍比这个两位数的“凸数”小132,请求出这个两位数.
科目:初中数学 来源: 题型:
【题目】有四张相同的卡片,分别写有数字![]() 2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
(1)从中任意抽出一张,抽到卡片上的数字为负数的概率;
(2)从中任意抽出两张,用树状图或表格列出所有可能的结果,并求抽出卡片上的数字积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点A、B、C均在格点上,在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度直尺画出点P(保留画图痕迹)
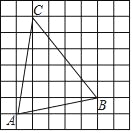
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示:

(1)求y(千克)与销售价z的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数﹣5,|﹣1.5|,﹣![]() ,0,3
,0,3![]() ,﹣(﹣1)表示的点.
,﹣(﹣1)表示的点.
(1)画在数轴上;
(2)用“<”把这些数连接起来;
(3)指出:负数是 ;分数是 ;非负整数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元3世纪,古希腊数学家丢番图(Diophantus)在其《算术》一书中设置了以下问题:已知两正整数之和为20,乘积为96,求这两个数.因为两数之和为20,所以这两个数不可能同时大于10,也不可能同时小于10,必定是一个大于10,一个小于10.根据如图所示的设法,可设一个数为![]() ,则另一个数为
,则另一个数为![]() ,根据两数之积为96,可得
,根据两数之积为96,可得![]() .请根据以上思路解决下列问题:
.请根据以上思路解决下列问题:
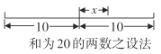
(1)若两个正整数之和为100,大数比小数大![]() ,根据丢番图的设法,这两个正整数可表示为____和___;
,根据丢番图的设法,这两个正整数可表示为____和___;
(2)请你根据丢番图的运算方法,计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
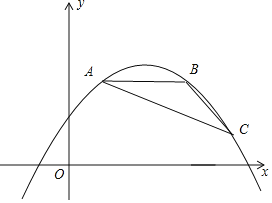
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2,下列图象中大致反映y与x之间的函数关系的是( )
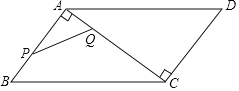
A. 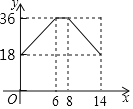 B.
B. 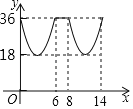
C. 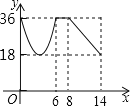 D.
D. 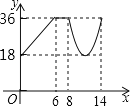
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com