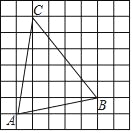
【题目】在每个小正方形的边长为1的网格中，点A、B、C均在格点上，在△ABC的内部有一点P，满足S△PAB：S△PBC：S△PCA=1：2：3，请在如图所示的网格中，用无刻度直尺画出点P（保留画图痕迹）
【答案】画图见解析.
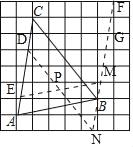
【解析】 如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N，G．连接DN，EM，DG，DN与EM相交于点P，点P即为所求．
∵平行四边形ABME的面积：平行四边形CDNB的面积：平行四边形DEMG的面积=1：2：3，△PAB的面积=
平行四边形ABME的面积，△PBC的面积=平行四边形CDNB的面积，△PAC的面积=△PNG的面积=△DGN的面积=平行四边形DEMG的面积，
∴S△PAB：S△PBC：S△PCA=1：2：3．
如图所示：如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N，G．连接DN，EM，DG，DN与EM相交于点P，点P即为所求．
科目：初中数学 来源： 题型：
【题目】已知直线l1：y=（k﹣1）x+k+1和直线l2：y=kx+k+2，其中k为不小于2的自然数．
（1）当k=2时，直线l1、l2与x轴围成的三角形的面积S2=______；
（2）当k=2、3、4，……，2018时，设直线l1、l2与x轴围成的三角形的面积分别为S2，S3，S4，……，S2018，则S2+S3+S4+……+S2018=______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，∠1=∠2．求证：∠3 +∠4=180°．
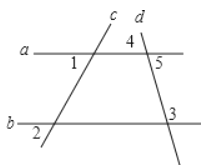
证明：∵∠1=∠2（已知）
∴ a∥b（ ）
∴∠3 +∠5=180° （两直线平行，同旁内角互补）
又 ∵∠4=∠5 （ ）
∴∠3 +∠4=180° （等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】CD经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠
，
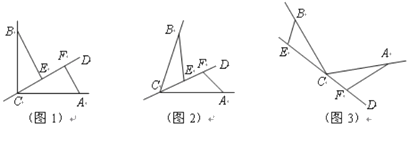
（1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°,∠=90°，则BE_____CF；EF____
.（填“＞”“＜”或“=”）
②如图2，若0°＜∠BCA＜180°,请添加一个关于∠与∠BCA关系的条件__________,使①中的两个结论仍然成立，并证明两个结论成立.
（2）如图3，若直线CD经过∠BCA的外部，∠=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）.
查看答案和解析>>
科目：初中数学 来源： 题型：
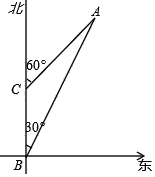
【题目】已知海岛A的周围6km的范围内有暗礁，一艘海轮在B处测得海岛A在北偏东30°的方向；向正北方向航行6km到达C处，又测得该岛在北偏东60°的方向，如果海轮不改变航向，继续向正北航行，有没有触礁的危险？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
材料一：对于一个两位数
，交换它的个位和十位数字得到的新数
叫这个两位数的“倒序数”.如：23的倒序数是32，50的倒序数是05.
材料二：对于一个两位数，若它的个位数字与十位数字的和小于等于9，则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数的“凸数”.如23的凸数是253.
（1）请求出42的“倒序数”与“凸数”；38有“凸数”吗？为什么？
（2）若一个两位数与它的“倒序数”的和的4倍比这个两位数的“凸数”小132，请求出这个两位数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
在数轴上5与
所对的两点之间的距离：
；
在数轴上与3所对的两点之间的距离：
；
在数轴上
与
所对的两点之间的距离：
；
在数轴上点
、
分别表示数
、
，则、两点之间的距离
回答下列问题：
（1）数轴上表示和的两点之间的距离是_________；
数轴上表示数
和3的两点之间的距离表示为_________；
数轴上表示数_______和________的两点之间的距离表为
；
（2）七年级研究性学习小组在数学老师指导下，对式子
进行探究：
①请你借助于数轴进行探究：当表示数的点在与3之间移动时，
的值总是一个固定的值为：____________．
②请你借助于数轴进行探究：如果要使
，那么数轴上表示点的数
__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
