
【题目】如图,已知AD∥BC,DC⊥BC, AE平分∠BAD, E为CD中点,试探索AD、BC和AB之间有何关系?并说明理由.
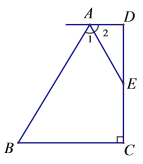
【答案】AD+BC=AB见解析;
【解析】
利用“AAS”可证明Rt△ADE≌Rt△AFE得到AD=AF,利用“HL”可证明Rt△BCE≌Rt△BFE得到BC=BF,于是有AD+BC=AF+BF=AB.
证明:过点E作EF⊥AB,连接BE
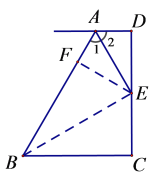
∵AD∥BC,DC⊥BC, EF⊥AB
∴∠D+∠C=180°,∠C=∠AFE=∠BFE=90°
∴∠D=∠AFE =90°.
∵AE平分∠BAD,
∴∠1=∠2
在△ADE和△AFE中
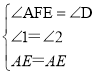
∴△ADE≌△AFE(AAS),
∴FE=DE,AD=AF
又∵E为CD中点
∴DE=CE,
∴FE =CE,
在Rt△BEF和Rt△BEC中,![]()
![]()
∴Rt△ BEF≌Rt△ BEC(HL),
∴BF= BC
∴AD+BC=AF+BF=AB.


科目:初中数学 来源: 题型:
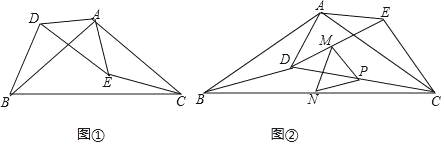
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点A、B、C均在格点上,在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度直尺画出点P(保留画图痕迹)
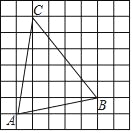
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数﹣5,|﹣1.5|,﹣![]() ,0,3
,0,3![]() ,﹣(﹣1)表示的点.
,﹣(﹣1)表示的点.
(1)画在数轴上;
(2)用“<”把这些数连接起来;
(3)指出:负数是 ;分数是 ;非负整数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元3世纪,古希腊数学家丢番图(Diophantus)在其《算术》一书中设置了以下问题:已知两正整数之和为20,乘积为96,求这两个数.因为两数之和为20,所以这两个数不可能同时大于10,也不可能同时小于10,必定是一个大于10,一个小于10.根据如图所示的设法,可设一个数为![]() ,则另一个数为
,则另一个数为![]() ,根据两数之积为96,可得
,根据两数之积为96,可得![]() .请根据以上思路解决下列问题:
.请根据以上思路解决下列问题:
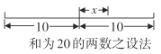
(1)若两个正整数之和为100,大数比小数大![]() ,根据丢番图的设法,这两个正整数可表示为____和___;
,根据丢番图的设法,这两个正整数可表示为____和___;
(2)请你根据丢番图的运算方法,计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
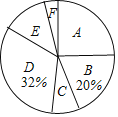
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分.
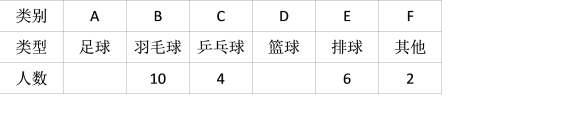
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜欢乒乓球的有 人,最喜欢篮球的学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,其中,最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %;
(3)该校共有450名学生,根据调查结果,估计该校最喜欢排球的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
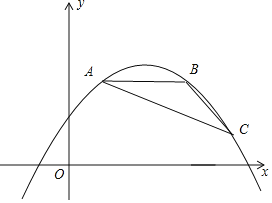
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 、16,点
、16,点![]() 为数轴上一动点,点
为数轴上一动点,点![]() 对应的数为
对应的数为![]() .
.
(1)填空:若![]() 时,点
时,点![]() 到点
到点![]() 、点
、点![]() 的距离之和为_____________.
的距离之和为_____________.
(2)填空:若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,则
的距离相等,则![]() _______.
_______.
(3)填空:若![]() ,则
,则![]() _______.
_______.
(4)若动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向点
向点![]() 运动,动点
运动,动点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向点
向点![]() 运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过
运动两动点同时运动且一动点到达终点时另一动点也停止运动,经过![]() 秒
秒![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:①-1是1的平方根。②带根号的数都是无理数。③-1的立方根是-1。④![]() 的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com