
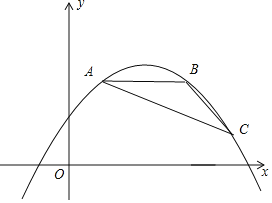
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
【答案】(1)(m,2m﹣5);(2)S△ABC =﹣![]() ;(3)m的值为
;(3)m的值为![]() 或10+2
或10+2![]() .
.
【解析】(1)利用配方法将二次函数解析式由一般式变形为顶点式,此题得解;
(2)过点C作直线AB的垂线,交线段AB的延长线于点D,由AB∥x轴且AB=4,可得出点B的坐标为(m+2,4a+2m5),设BD=t,则点C的坐标为(m+2+t,4a+2m5t),利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之取其正值即可得出t值,再利用三角形的面积公式即可得出S△ABC的值;
(3)由(2)的结论结合S△ABC=2可求出a值,分三种情况考虑:①当m>2m2,即m<2时,x=2m2时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元二次方程,解之可求出m的值;②当2m5≤m≤2m2,即2≤m≤5时,x=m时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元一次方程,解之可求出m的值;③当m<2m5,即m>5时,x=2m5时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元一次方程,解之可求出m的值.综上即可得出结论.
(1)∵y=ax2﹣2amx+am2+2m﹣5=a(x﹣m)2+2m﹣5,
∴抛物线的顶点坐标为(m,2m﹣5),
故答案为:(m,2m﹣5);
(2)过点C作直线AB的垂线,交线段AB的延长线于点D,如图所示,
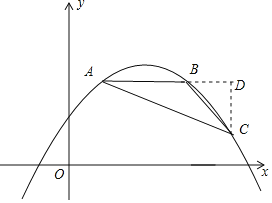
∵AB∥x轴,且AB=4,
∴点B的坐标为(m+2,4a+2m﹣5),
∵∠ABC=135°,
∴设BD=t,则CD=t,
∴点C的坐标为(m+2+t,4a+2m﹣5﹣t),
∵点C在抛物线y=a(x﹣m)2+2m﹣5上,
∴4a+2m﹣5﹣t=a(2+t)2+2m﹣5,
整理,得:at2+(4a+1)t=0,
解得:t1=0(舍去),t2=﹣![]() ,
,
∴S△ABC=![]() ABCD=﹣
ABCD=﹣![]() ;
;
(3)∵△ABC的面积为2,
∴﹣![]() =2,
=2,
解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x﹣m)2+2m﹣5.
(x﹣m)2+2m﹣5.
分三种情况考虑:
①当m>2m﹣2,即m<2时,有﹣![]() (2m﹣2﹣m)2+2m﹣5=2,
(2m﹣2﹣m)2+2m﹣5=2,
整理,得:m2﹣14m+39=0,
解得:m1=7﹣![]() (舍去),m2=7+
(舍去),m2=7+![]() (舍去);
(舍去);
②当2m﹣5≤m≤2m﹣2,即2≤m≤5时,有2m﹣5=2,解得:m=![]() ;
;
③当m<2m﹣5,即m>5时,有﹣![]() (2m﹣5﹣m)2+2m﹣5=2,
(2m﹣5﹣m)2+2m﹣5=2,
整理,得:m2﹣20m+60=0,
解得:m3=10﹣2![]() (舍去),m4=10+2
(舍去),m4=10+2![]() .
.
综上所述:m的值为![]() 或10+2
或10+2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2.求证:∠3 +∠4=180°.
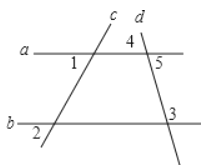
证明:∵∠1=∠2(已知)
∴ a∥b( )
∴∠3 +∠5=180° (两直线平行,同旁内角互补)
又 ∵∠4=∠5 ( )
∴∠3 +∠4=180° (等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料一:对于一个两位数![]() ,交换它的个位和十位数字得到的新数
,交换它的个位和十位数字得到的新数![]() 叫这个两位数
叫这个两位数![]() 的“倒序数”.如:23的倒序数是32,50的倒序数是05.
的“倒序数”.如:23的倒序数是32,50的倒序数是05.
材料二:对于一个两位数![]() ,若它的个位数字与十位数字的和小于等于9,则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数
,若它的个位数字与十位数字的和小于等于9,则把个位数字与十位数字的和插入到这个两位数中间得到的新数叫这个两位数![]() 的“凸数”.如23的凸数是253.
的“凸数”.如23的凸数是253.
(1)请求出42的“倒序数”与“凸数”;38有“凸数”吗?为什么?
(2)若一个两位数与它的“倒序数”的和的4倍比这个两位数的“凸数”小132,请求出这个两位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
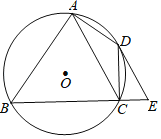
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:
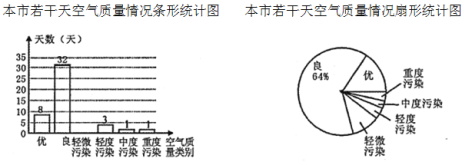
(1)通过计算补全条形统计图;
(2)求扇形统计图中表示“轻度污染”的扇形的圆心角度数;
(3)请估计我市这一年(365天)达到“优”和“良”的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数轴上5与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() ;
;
在数轴上![]() 与3所对的两点之间的距离:
与3所对的两点之间的距离:![]() ;
;
在数轴上![]() 与
与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() ;
;
在数轴上点![]() 、
、![]() 分别表示数
分别表示数![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]()
![]()
回答下列问题:
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是_________;
的两点之间的距离是_________;
数轴上表示数![]() 和3的两点之间的距离表示为_________;
和3的两点之间的距离表示为_________;
数轴上表示数_______和________的两点之间的距离表为![]() ;
;
(2)七年级研究性学习小组在数学老师指导下,对式子![]() 进行探究:
进行探究:
①请你借助于数轴进行探究:当表示数![]() 的点在
的点在![]() 与3之间移动时,
与3之间移动时,![]() 的值总是一个固定的值为:____________.
的值总是一个固定的值为:____________.
②请你借助于数轴进行探究:如果要使![]() ,那么数轴上表示点的数
,那么数轴上表示点的数![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com