
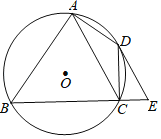
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
【答案】(1)证明见解析;(2)AC的长为![]() .
.
【解析】(1)先判断出BD是圆O的直径,再判断出BD⊥DE,即可得出结论;
(2)先判断出AC⊥BD,进而求出BC=AB=8,进而判断出△BCD∽△DCE,求出CD,再用勾股定理求出BD,最后判断出△CFD∽△BCD,即可得出结论.
(1)如图,连接BD,

∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°.
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°.
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵DE∥AC.
∵∠BDE=90°,
∴∠BFC=90°,
∴CB=AB=8,AF=CF=![]() AC,
AC,
∵∠CDE+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠CDE=∠CBD.
∵∠DCE=∠BCD=90°,
∴△BCD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=4.
在Rt△BCD中,BD=![]() =4
=4![]() ,
,
同理:△CFD∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴CF=![]() ,
,
∴AC=2AF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示:

(1)求y(千克)与销售价z的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元3世纪,古希腊数学家丢番图(Diophantus)在其《算术》一书中设置了以下问题:已知两正整数之和为20,乘积为96,求这两个数.因为两数之和为20,所以这两个数不可能同时大于10,也不可能同时小于10,必定是一个大于10,一个小于10.根据如图所示的设法,可设一个数为![]() ,则另一个数为
,则另一个数为![]() ,根据两数之积为96,可得
,根据两数之积为96,可得![]() .请根据以上思路解决下列问题:
.请根据以上思路解决下列问题:
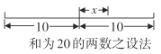
(1)若两个正整数之和为100,大数比小数大![]() ,根据丢番图的设法,这两个正整数可表示为____和___;
,根据丢番图的设法,这两个正整数可表示为____和___;
(2)请你根据丢番图的运算方法,计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,发生的概率是![]() 的是( )
的是( )
A.从一副扑克牌中,任意抽取其中的一张,抽到红桃的概率
B.一个圆盘被染成红、黄、蓝、紫四种颜色,随机转动一次,转盘停止时,指针刚好指向红色的概率
C.小明开车到十字路口时,遇到红灯的概率
D.一道单选题有![]() 四个备用选项, 从中随机选一个作答,答对的概率
四个备用选项, 从中随机选一个作答,答对的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
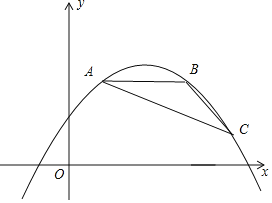
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com