
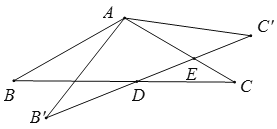
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.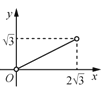 B.
B.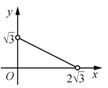 C.
C.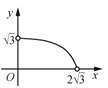 D.
D.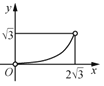
【答案】B
【解析】
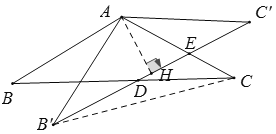
连接B′C,作AH⊥B′C′,垂足为H,由已知以及旋转的性质可得AB′=AB=AC=AC′=2,∠AB′C′=∠C′=30°,继而可求出AH长,B′C′的长,由等腰三角形的性质可得∠AB′C=∠ACB′,再根据∠AB′D=∠ACD=30°,可得∠DB′C=∠DCB′,从而可得B′D=CD,进而可得 B′E=x,由此可得C′E=2![]() -x,再根据三角形面积公式即可求得y与x的关系式,由此即可得到答案.
-x,再根据三角形面积公式即可求得y与x的关系式,由此即可得到答案.
连接B′C,作AH⊥B′C′,垂足为H,
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∵△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,
∴AB′=AB=AC=AC′=2,∠AB′C′=∠C′=30°,
∴AH=![]() AC′=1,
AC′=1,
∴C′H=![]() ,
,
∴B′C′=2C′H=2![]() ,
,
∵AB′=AC,
∴∠AB′C=∠ACB′,
∵∠AB′D=∠ACD=30°,
∴∠AB′C-∠AB′D=∠ACB′-∠ACD,
即∠DB′C=∠DCB′,
∴B′D=CD,
∵CD+DE=x,
∴B′D+DE=x,即B′E=x,
∴C′E=B′C′-B′E=2![]() -x,
-x,
∴y=![]() =
=![]() ×(2
×(2![]() -x)×1=
-x)×1=![]() ,
,
观察只有B选项的图象符合题意,
故选B.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】广州融创乐园是国内首个以南越文化、岭南风格为主题的游乐园,自2019年6月开园以来受到了国内外游客的热捧.某旅游团组织一批游客游玩了乐园内的四个网红项目,“A.双龙飞舞”、“B.飞跃广东”、“C.云霄塔”、“D.怒海狂涛”,并进行了“我最喜欢的一个项目”的投票评选活动,投票结果绘制成以下两幅尚未完整的统计图.请你根据图中提供的信息,解答下列问题:
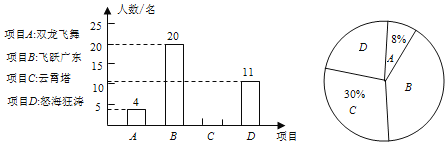
(1)参与投票的游客总人数为 人;
(2)扇形统计图中B所对的圆心角度数为 度,并补全条形统计图;
(3)从投票给“双龙飞舞“的3名男生和1名女生中随机抽取2名了解情况,请你用列举法求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C为线段![]() 上一点,以
上一点,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,在
,在![]() 外侧,以
外侧,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() .
.
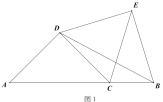
(1)如图1,当![]() 时:
时:
①求证:![]() ;
;
②判断线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
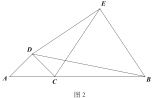
(2)如图2,当![]() 时,
时,![]() 与
与![]() 的数量关系是否保持不变?
的数量关系是否保持不变?
对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:
想法1:尝试将点D为旋转中心,过点D作线段![]() 垂线,交
垂线,交![]() 延长线于点G,连接
延长线于点G,连接![]() ;通过证明
;通过证明![]() 解决以上问题;
解决以上问题;
想法2:尝试将点D为旋转中心,过点D作线段![]() 垂线,垂足为点G,连接
垂线,垂足为点G,连接![]() .通过证明
.通过证明![]() 解决以上问题;
解决以上问题;
想法3:尝试利用四点共圆,过点D作![]() 垂线段
垂线段![]() ,连接
,连接![]() ,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
请你参考上面的想法,证明![]() (一种方法即可).
(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.
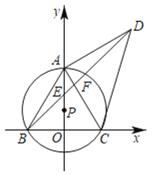
(1)求证:AB=AD;
(2)若BF=4,DF=6,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元
(1)求每台A型加湿器和B型加湿器的销售利润;
(2)该商店计划一次购进两种型号的加湿器共100台,其中B型加湿器的进货量不超过A型加湿器的2倍,设购进A型加湿器x台.这100台加湿器的销售总利润为y元
①求y关于x的函数关系式;
②该商店应怎样进货才能使销售总利润最大?
(3)实际进货时,厂家对A型加湿器出厂价下调m(0<m<100)元,且限定商店最多购进A型加湿器70台,若商店保持两种加湿器的售价不变,请你根据以上信息及(2)中条件,设计出使这100台加湿器销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
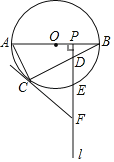
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,试证明四边形
,试证明四边形![]() 为菱形;
为菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一大、一小两个等腰直角三角形拼在一起,![]() ,连接
,连接![]() .
.
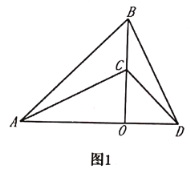
(1)如图1,若![]() 三点在同一条直线上,则
三点在同一条直线上,则![]() 与
与![]() 的关系是 ;
的关系是 ;
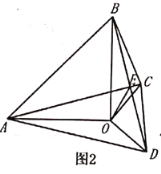
(2)如图2,若![]() 三点不在同一条直线上,
三点不在同一条直线上,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,猜想
,猜想![]() 之间的数量关系,并给予证明;
之间的数量关系,并给予证明;
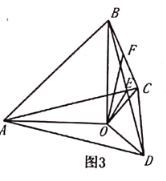
(3)如图3,在(2)的条件下作![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 与
与![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
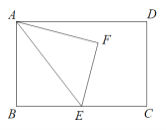
【题目】如图,在矩形ABCD中,AB=10,BC=m,E为BC边上一点,沿AE翻折△ABE,点B落在点F处.
(1)连接CF,若CF//AE,求EC的长(用含m的代数式表示);
(2)若EC=![]() ,当点F落在矩形ABCD的边上时,求m的值;
,当点F落在矩形ABCD的边上时,求m的值;
(3)连接DF,在BC边上是否存在两个不同位置的点E,使得?若存![]() 在,直接写出m的取值范围;若不存在,说明理由.
在,直接写出m的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com