
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γœζ έ10Χ®A–ΆΚΆ20Χ®B–ΆΦ” ΣΤςΒΡάϊ»σΈΣ2500‘ΣΘ§œζ έ20Χ®A–ΆΚΆ10Χ®B–ΆΦ” ΣΤςΒΡάϊ»σΈΣ2000‘Σ
(1)«σΟΩΧ®A–ΆΦ” ΣΤςΚΆB–ΆΦ” ΣΤςΒΡœζ έάϊ»σΘΜ
(2)ΗΟ…ΧΒξΦΤΜ°“Μ¥ΈΙΚΫχΝΫ÷÷–ΆΚ≈ΒΡΦ” ΣΤςΙ≤100Χ®Θ§Τδ÷–B–ΆΦ” ΣΤςΒΡΫχΜθΝΩ≤Μ≥§ΙΐA–ΆΦ” ΣΤςΒΡ2±ΕΘ§…ηΙΚΫχA–ΆΦ” ΣΤςxΧ®Θ°’β100Χ®Φ” ΣΤςΒΡœζ έΉήάϊ»σΈΣy‘Σ
ΔΌ«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎΗΟ…ΧΒξ”Π‘θ―υΫχΜθ≤≈Ρή Ιœζ έΉήάϊ»σΉν¥σ?
(3) ΒΦ ΫχΜθ ±Θ§≥ßΦ“Ε‘A–ΆΦ” ΣΤς≥ω≥ßΦέœ¬Βςm(0<m<100)‘ΣΘ§«“œόΕ®…ΧΒξΉνΕύΙΚΫχA–ΆΦ” ΣΤς70Χ®Θ§»τ…ΧΒξ±Θ≥÷ΝΫ÷÷Φ” ΣΤςΒΡ έΦέ≤Μ±δΘ§«κΡψΗυΨί“‘…œ–≈œΔΦΑ(2)÷–ΧθΦΰΘ§…ηΦΤ≥ω Ι’β100Χ®Φ” ΣΤςœζ έΉήάϊ»σΉν¥σΒΡΫχΜθΖΫΑΗΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΩΧ®A–ΆΦ” ΣΤςΚΆB–ΆΦ” ΣΤςΒΡœζ έάϊ»σΖ÷±πΈΣ50‘ΣΘ§100‘ΣΘ°Θ®2Θ©ΔΌy=10000-50xΘΜΔΎAΫχ34Χ® ±Θ§άϊ»σΉν¥σΘ§Ήν¥σ÷ΒΈΣΘΚ8300‘ΣΘΜΘ®3Θ©ΔΌm=50 ±Θ§y=10000Θ§¥Υ ±x»Γ34÷Ν70Φδ»Έ“β’ϊ ΐΨυΩ…ΘΜΔΎA–ΆΫχΜθ70Χ®Θ§B–ΆΫχΜθ30Χ®ΘΜΔέA–ΆΫχΜθ30Χ®Θ§B–ΆΫχΜθ70Χ®Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΟΩΧ®A–ΆΦ” ΣΤςΚΆB–ΆΦ” ΣΤςΒΡœζ έάϊ»σΖ÷±πΈΣx‘ΣΓΔy‘ΣΘ§»ΜΚσΗυΨίΧβ“βΝ–≥ω“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΉιΫβ¥πΦ¥Ω…ΘΜ
Θ®2Θ©ΔΌΨίΧβ“βΒΟΦ¥Ω…»ΖΕ®yΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎœ»ΗυΨίΧβ“βΝ–≤ΜΒ» Ϋ«σ≥ωxΒΡΖΕΈßΘ§‘ΌΗυΨί“Μ¥ΈΚ· ΐΒΡ‘ωΦθ–‘Ϋβ¥πΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΧβ“βΝ–≥ωΚ· ΐ ΐΙΊœΒ ΫΘ§Ζ÷“‘œ¬»ΐ÷÷«ιΩωΔΌ0<m<50Θ§ΔΎm=50Θ§Δέ 50 <m < 100 ±Θ§m-50 >0Ζ÷±πΫχ––«σΫβΦ¥Ω…Θ°
Θ®1Θ©Ϋβ…ηΟΩΧ®A–ΆΦ” ΣΤςΚΆB–ΆΦ” ΣΤςΒΡœζ έάϊ»σΖ÷±πΈΣx‘ΣΓΔy‘ΣΘ§
”…Χβ“βΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Φ¥ΟΩΧ®A–ΆΦ” ΣΤςΚΆB–ΆΦ” ΣΤςΒΡœζ έάϊ»σΖ÷±πΈΣ50‘ΣΘ§100‘ΣΘ°
Θ®2Θ©ΔΌΨίΧβ“βΒΟΦ¥Ω…»ΖΕ®yΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΈΣy=50x+100Θ®100-xΘ©=10000-50xΘΜ
ΔΎ”…Χβ“βΒΟ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
ΓΏ-50<0Θ§
ΓύyΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΓύΒ±x=34 ±Θ§y»ΓΉν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣΘΚ8300‘ΣΘ°
Θ®3Θ©”…Χβ“βΒΟΘΚy=(50+m)x+100Θ®100-xΘ©=10000+(m-50)xΘ§
Τδ÷–![]() Θ§
Θ§
ΔΌΒ±m-50=0 ±Θ§Φ¥m=50 ±Θ§y=10000Θ§¥Υ ±x»Γ34÷Ν70Φδ»Έ“β’ϊ ΐΨυΩ…ΘΜ
ΔΎΒ±m-50>0 ±Θ§Φ¥100>m>50 ±Θ§yΥφx‘ω¥σΕχ‘ω¥σΘ§¥Υ ±x= 70 ±Θ§œζ έάϊ»σΉν¥σΘ§Φ¥A–ΆΫχΜθ70Χ®Θ§B–ΆΫχΜθ30Χ®ΘΜ
ΔέΒ±m-50<0 ±Θ§Φ¥0<m<50 ±Θ§yΥφx‘ω¥σΕχΦθ–ΓΘ§¥Υ ±x= 30 ±Θ§œζ έάϊ»σΉν¥σΘ§Φ¥A–ΆΫχΜθ30Χ®Θ§B–ΆΫχΜθ70Χ®Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
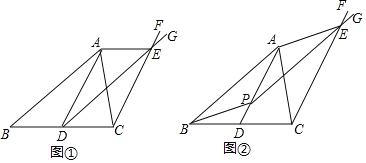
ΓΨΧβΡΩΓΩ»γΆΦΘ§AD «ΓςABCΒΡ÷–œΏΘ§ΙΐΒψCΉς÷±œΏCFΓΈADΘ°
Θ®Έ ΧβΘ©»γΆΦΔΌΘ§ΙΐΒψDΉς÷±œΏDGΓΈABΫΜ÷±œΏCF”ΎΒψEΘ§Ν§ΫαAEΘ§«σ÷ΛΘΚABΘΫDEΘ°
Θ®ΧΫΨΩΘ©»γΆΦΔΎΘ§‘ΎœΏΕΈAD…œ»Έ»Γ“ΜΒψPΘ§ΙΐΒψPΉς÷±œΏPGΓΈABΫΜ÷±œΏCF”ΎΒψEΘ§Ν§ΫαAEΓΔBPΘ§ΧΫΨΩΥΡ±Ώ–ΈABPE «ΡΡάύΧΊ βΥΡ±Ώ–Έ≤ΔΦ”“‘÷ΛΟςΘ°
Θ®”Π”ΟΘ©‘ΎΧΫΨΩΒΡΧθΦΰœ¬Θ§…ηPEΫΜAC”ΎΒψMΘ°»τΒψP «ADΒΡ÷–ΒψΘ§«“ΓςAPMΒΡΟφΜΐΈΣ1Θ§÷±Ϋ”–¥≥ωΥΡ±Ώ–ΈABPEΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
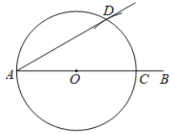
ΓΨΧβΡΩΓΩœ¬Οφ «ΓΑΉς“ΜΗω![]() Ϋ«Γ±ΒΡ≥ΏΙφΉςΆΦΙΐ≥ΧΘ°
Ϋ«Γ±ΒΡ≥ΏΙφΉςΆΦΙΐ≥ΧΘ°
“―÷ΣΘΚΤΫΟφΡΎ“ΜΒψAΘ°
«σΉςΘΚ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Θ°
Θ°
ΉςΖ®ΘΚ»γΆΦΘ§
Θ®1Θ©Ής…δœΏ![]() ΘΜ
ΘΜ
Θ®2Θ©‘Ύ…δœΏ![]() »Γ“ΜΒψOΘ§“‘OΈΣ‘≤–ΡΘ§
»Γ“ΜΒψOΘ§“‘OΈΣ‘≤–ΡΘ§![]() ΈΣΑκΨΕΉς‘≤Θ§”κ…δœΏ
ΈΣΑκΨΕΉς‘≤Θ§”κ…δœΏ![]() œύΫΜ”ΎΒψCΘΜ
œύΫΜ”ΎΒψCΘΜ
Θ®3Θ©“‘CΈΣ‘≤–ΡΘ§![]() CΈΣΑκΨΕΉςΜΓΘ§”κ
CΈΣΑκΨΕΉςΜΓΘ§”κ![]() ΫΜ”ΎΒψDΘ§Ής…δœΏ
ΫΜ”ΎΒψDΘ§Ής…δœΏ![]() Θ°
Θ°
‘ρ![]() Φ¥ΈΣΥυ«σΒΡΫ«Θ°
Φ¥ΈΣΥυ«σΒΡΫ«Θ°
«κΜΊ¥πΘΚΗΟ≥ΏΙφΉςΆΦΒΡ“άΨί «_________________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓ―OΒΡΑκΨΕ «2Θ§ΒψAΓΔBΓΔC‘ΎΓ―O…œΘ§»τΥΡ±Ώ–ΈOABCΈΣΝβ–ΈΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΟφΜΐΈΣΘ®ΓΓΓΓΘ©
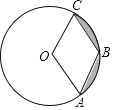
A.![]() Π–©¹2
Π–©¹2![]() B.
B.![]() Π–©¹
Π–©¹![]() C.
C.![]() Π–©¹2
Π–©¹2![]() D.
D.![]() Π–©¹
Π–©¹![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
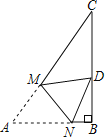
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣRtΓςABC÷–Θ§ΓœBΘΫ90ΓψΘ§ΓœAΘΫ60ΓψΘ§ABΘΫ3Θ§ΒψMΘ§NΖ÷±π‘ΎœΏΕΈACΘ§AB…œΘ§ΫΪΓςANM―Ί÷±œΏMN’έΒΰΘ§ ΙΒψAΒΡΕ‘”ΠΒψD«ΓΚΟ¬δ‘ΎœΏΕΈBC…œΘ§»τΓςDCMΈΣ÷±Ϋ«»ΐΫ«–Έ ±Θ§‘ρAMΒΡ≥ΛΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§AB=AC=2Θ§ΓœB=30ΓψΘ§ΓςABC»ΤΒψAΡφ ±’κ–ΐΉΣΠΝ(0<ΠΝ<120Γψ)ΒΟΒΫ![]() Θ§
Θ§![]() ”κBCΘ§ACΖ÷±πΫΜ”ΎΒψDΘ§E.…η
”κBCΘ§ACΖ÷±πΫΜ”ΎΒψDΘ§E.…η![]() Θ§
Θ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ”κ
”κ![]() ΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣ( )
ΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣ( )
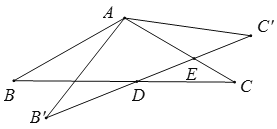
A.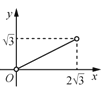 B.
B.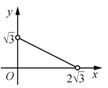 C.
C.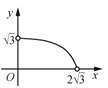 D.
D.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί±Ώ
ΩΣ Φ―Ί±Ώ![]() œρΒψ
œρΒψ![]() “‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ε·Βψ
“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί±Ώ
ΩΣ Φ―Ί±Ώ![]() œρΒψ
œρΒψ![]() “‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§ΙΐΒψ
“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§ΙΐΒψ![]() Ής
Ής![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°Βψ
Θ°Βψ![]() Ζ÷±π¥”Βψ
Ζ÷±π¥”Βψ![]() Ά§ ±≥ωΖΔΘ§Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤Υφ÷°ΆΘ÷Ι‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣ
Ά§ ±≥ωΖΔΘ§Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤Υφ÷°ΆΘ÷Ι‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣ![]() Οκ
Οκ![]() Θ°
Θ°
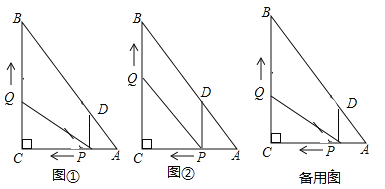
Θ®1Θ©»γΆΦΔΌΘ§÷±Ϋ””ΟΚ§![]() ΒΡ¥ζ ΐ ΫΖ÷±π±μ ΨΘΚ
ΒΡ¥ζ ΐ ΫΖ÷±π±μ ΨΘΚ![]() ΓΓ ΓΓΘ§
ΓΓ ΓΓΘ§![]() ______Θ§
______Θ§
Θ®2Θ©»γΆΦΔΎΘ§
ΔΌΒ±![]() _____Οκ ±Θ§ΥΡ±Ώ–Έ
_____Οκ ±Θ§ΥΡ±Ώ–Έ![]() ΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
ΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
ΔΎ «Ζώ¥φ‘Ύ![]() ΒΡ÷ΒΘ§ ΙΥΡ±Ώ–Έ
ΒΡ÷ΒΘ§ ΙΥΡ±Ώ–Έ![]() ΈΣΝβ–ΈΘΩ»τ¥φ‘ΎΘ§–¥≥ω
ΈΣΝβ–ΈΘΩ»τ¥φ‘ΎΘ§–¥≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κ«σ≥ωΒ±Βψ
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κ«σ≥ωΒ±Βψ![]() ΒΡΥΌΕ»Θ®‘»ΥΌ‘ΥΕ·Θ©±δΈΣΟΩΟκΕύ…ΌΗωΒΞΈΜ≥ΛΕ» ±Θ§≤≈Ρή ΙΥΡ±Ώ–Έ
ΒΡΥΌΕ»Θ®‘»ΥΌ‘ΥΕ·Θ©±δΈΣΟΩΟκΕύ…ΌΗωΒΞΈΜ≥ΛΕ» ±Θ§≤≈Ρή ΙΥΡ±Ώ–Έ![]() ‘ΎΡ≥“Μ ±ΩΧ≥…ΈΣΝβ–ΈΘΩ
‘ΎΡ≥“Μ ±ΩΧ≥…ΈΣΝβ–ΈΘΩ
Θ®3Θ©…η![]() ΒΡΆβΫ”‘≤ΟφΜΐΈΣ
ΒΡΆβΫ”‘≤ΟφΜΐΈΣ![]() Θ§«σ≥ω
Θ§«σ≥ω![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ≈–ΕœΒ±
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ≈–ΕœΒ±![]() Ήν–Γ ±Θ§
Ήν–Γ ±Θ§![]() ΒΡΆβΫ”‘≤”κ÷±œΏ
ΒΡΆβΫ”‘≤”κ÷±œΏ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ«“ΥΒΟςάμ”…Θ°
ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ«“ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§≈ΉΈοœΏ
÷–Θ§≈ΉΈοœΏ![]() ΒΡΕΞΒψΈΣ
ΒΡΕΞΒψΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ≈ΉΈοœΏΫΜ”ΎΒψ
”κ≈ΉΈοœΏΫΜ”ΎΒψ![]() (Βψ
(Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡΉσ≤ύ)Θ°
ΒΡΉσ≤ύ)Θ°

Θ®1Θ©«σΒψ![]() Ήχ±ξΘΜ
Ήχ±ξΘΜ
Θ®2Θ©ΚαΓΔΉίΉχ±ξΕΦ «’ϊ ΐΒΡΒψΫ–Ήω’ϊΒψΘ°Φ«œΏΕΈ![]() ΦΑ≈ΉΈοœΏ‘Ύ
ΦΑ≈ΉΈοœΏ‘Ύ![]() ΝΫΒψ÷°ΦδΒΡ≤ΩΖ÷Έß≥…ΒΡΖβ±’«χ”ρ(≤ΜΚ§±ΏΫγ)Φ«ΈΣ
ΝΫΒψ÷°ΦδΒΡ≤ΩΖ÷Έß≥…ΒΡΖβ±’«χ”ρ(≤ΜΚ§±ΏΫγ)Φ«ΈΣ![]() Θ°
Θ°
ΔΌΒ±![]() ±Θ§ΫαΚœΚ· ΐΆΦœσΘ§÷±Ϋ”–¥≥ω«χ”ρ
±Θ§ΫαΚœΚ· ΐΆΦœσΘ§÷±Ϋ”–¥≥ω«χ”ρ![]() ΡΎΒΡ’ϊΒψΗω ΐΘΜ
ΡΎΒΡ’ϊΒψΗω ΐΘΜ
ΔΎ»γΙϊ«χ”ρ![]() ΡΎ”–2Ηω’ϊΒψΘ§«κ«σ≥ω
ΡΎ”–2Ηω’ϊΒψΘ§«κ«σ≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCD «Γ―OΒΡΡΎΫ”ΥΡ±Ώ–ΈΘ§BC «Γ―OΒΡ÷±ΨΕΘ§OEΓΆBCΫΜAB”ΎΒψEΘ§»τBE=2AEΘ§‘ρΓœADC =_________ΓψΘ°
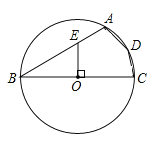
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com