
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.
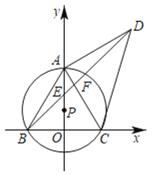
(1)求证:AB=AD;
(2)若BF=4,DF=6,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
【答案】(1)见解析;(2)2![]() ;(3)不发生变化,
;(3)不发生变化,![]()
【解析】
(1)先判断出△AOB≌△AOC(SAS),得出AB=AC,即可;
(2)过A作AM⊥BD于M,再判断出△ADM∽△FDA可求AD=![]() ,则CD=
,则CD=![]() ;
;
(3)不变,过D作DH⊥y轴于H,作DQ⊥x轴于Q,再证△DHA≌△AOC(AAS),得DH=AO,AH=OC,进而得出HO=BQ,所以DQ=BQ,即△DBQ为等腰直角三角形即可.
(1)证明:∵OA⊥BC,且OA过圆心点P,
∴OB=OC,
在△AOB和△AOC中,
 ,
,
∴△AOB≌△AOC(SAS),
∴AB=AC,
∵以AC为直角边作等腰Rt△ACD,
∴AD=AC,
∴AB=AD;
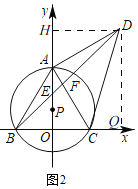
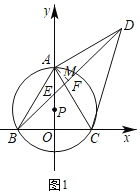
(2)如图1,过点A作AM⊥BD于M,
由(1)知,AB=AD,
∴DM=![]() BD,
BD,
∵BF=4,DF=6,
∴BD=10,
∴DM=5,
∵∠AMD=90°=∠DAF,∠ADM=∠FDA,
∴△ADM∽△FDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
在等腰直角三角形ADC中,CD=![]() AD=2
AD=2![]() ;
;
(3)![]() 的值是不发生变化,
的值是不发生变化,
理由:如图2,过点D作DH⊥y轴于H,作DQ⊥x轴于Q,
∴∠AHD=90°=∠COA,
∴∠ADH+∠DAH=90°,
∵∠CAD=90°,
∴∠CAO+∠DAH=90°,
∴∠ADH=∠CAO,
∵AD=AC,
∴△ADH≌△ACO(AAS),
∴DH=AO,AH=OC,
∵∠OHD=∠QOH=∠OQD=90°,
∴四边形OQDH是矩形,DH=OQ,DQ=OH,
又∵HO=AH+AO=OC+DH=OB+DH=OB+OQ=BQ,
∴DQ=BQ,
∴△DBQ为等腰直角三角形,
∴∠DBQ=45°,
∴∠DEH=∠BEO=45°,
∴sin∠DEH=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】今年的新冠疫情爆发,使很多农作物积压没法正常销售。为解决农民的困难,我市某食品加工公司主动分两次采购了一批竹笋, 第一次花费40万元,第二次花费60万元。已知第一次采购时每百千克竹笋的价格比去年的平均价格上涨了500元,第二次采购时每百千克竹笋的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每百千克竹笋的平均价格是多少元;
(2)该公司可将竹笋加工成笋干或罐头(湿笋),若单独加工成笋干,每天可加工8百千克竹笋,每百千克竹笋获利1000元; 若单独加工成罐头,每天可加工12百千克竹笋,每百千克竹笋获利600元,由于市场需要,所有采购的竹笋必需在30天内加工完毕,且加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,为获得最大利润,应将多少百千克竹笋加工成笋干?最大利润为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.
a.教育未来指数得分的频数分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
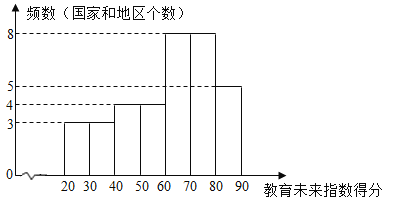
b.教育未来指数得分在![]() 这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c.35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图如下:
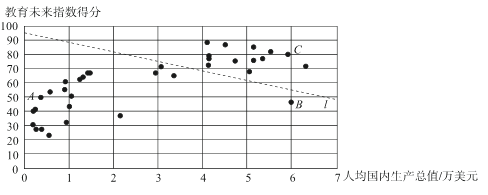
d.中国和中国香港的教育未来指数得分分别为32.9和68.5.
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第______;
(2)在35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○”画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为_____万美元;(结果保留一位小数)
(4)下列推断合理的是__________.(只填序号即可)
①相较于点![]() 所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
②相较于点![]() 所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
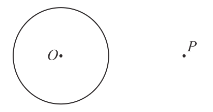
【题目】下面是小文设计的“过圆外一点作圆的切线”的作图过程.已知:![]() 和圆外一点
和圆外一点![]() .求作:过点
.求作:过点![]() 的
的![]() 的切线.作法:①连接
的切线.作法:①连接![]() ;②以
;②以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ;③作直线
;③作直线![]() ,
,![]() ;所以直线
;所以直线![]() ,
,![]() 为
为![]() 的切线.
的切线.
根据小文设计的作图过程,完成下面的证明.
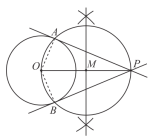
证明:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,
的直径,
∴![]() =∠________=________
=∠________=________
(________)(填推理的依据).
∴![]() ,________
,________![]() .
.
∵![]() ,
,![]() 为
为
∴直线![]() ,
,![]() 为
为![]() 的切线(________)(填推理的依据).
的切线(________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
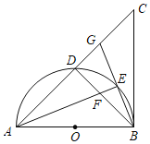
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以AB为直径的半圆O交AC于点D,点E是
,以AB为直径的半圆O交AC于点D,点E是![]() 上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:![]() ;
;
(2)填空:
①若![]() ,且点E是
,且点E是![]() 的中点,则DF的长为 ;
的中点,则DF的长为 ;
②取![]() 的中点H,当
的中点H,当![]() 的度数为 时,四边形OBEH为菱形.
的度数为 时,四边形OBEH为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
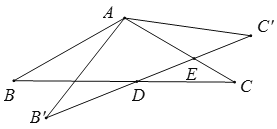
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.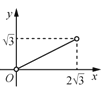 B.
B.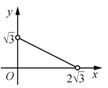 C.
C.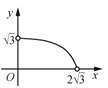 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
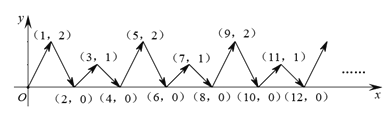
【题目】如图,动点![]() 在平面直角坐标系
在平面直角坐标系![]() 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点
中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点![]() 的坐标是( )
的坐标是( )
A.(26,0)B.(26,1)C.(27,1)D.(27,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
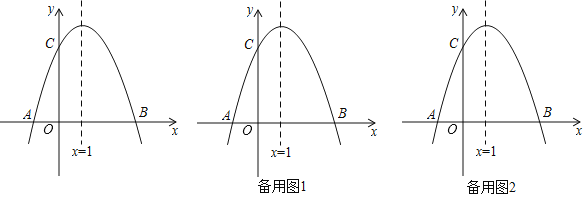
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com