
【题目】今年的新冠疫情爆发,使很多农作物积压没法正常销售。为解决农民的困难,我市某食品加工公司主动分两次采购了一批竹笋, 第一次花费40万元,第二次花费60万元。已知第一次采购时每百千克竹笋的价格比去年的平均价格上涨了500元,第二次采购时每百千克竹笋的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每百千克竹笋的平均价格是多少元;
(2)该公司可将竹笋加工成笋干或罐头(湿笋),若单独加工成笋干,每天可加工8百千克竹笋,每百千克竹笋获利1000元; 若单独加工成罐头,每天可加工12百千克竹笋,每百千克竹笋获利600元,由于市场需要,所有采购的竹笋必需在30天内加工完毕,且加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,为获得最大利润,应将多少百千克竹笋加工成笋干?最大利润为多少.
【答案】(1)3500元;(2)为获得最大利润,应将120百千克竹笋加工成笋干,最大利润为228000元
【解析】
(1)设去年每百千克竹笋是x元,则第一次采购的平均价格为(x+500)元,第二次采购的平均价格为(x-500)元,根据第二次的采购数量是第一次采购数量的两倍,据此列方程求解;
(2)先求出今年所采购竹笋总数量,根据所有采购的竹笋必需在30天内加工完毕,加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,据此列不等式组求解,在结合利润表达式,利用一次函数的性质求出最大利润.
(1)解:设去年每百千克竹笋单价为x,则第一次单价x+500,第二次单价x-500,由题
![]() ,得x=3500
,得x=3500
经检验,x=3500是原方程的解
∴去年每百千克竹笋单价为3500元
(2)二次采购竹笋总数量为:400000÷(3500+500)+600000÷(3500-500)=300百千克
设加工成笋干的竹笋为y百千克,加工成罐头为(300-y)百千克
依题意: 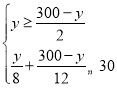
∴![]()
利润![]()
![]()
∵400>0
∴w随y增大而增大
∴当y=120时,![]() 元
元
综上,为获得最大利润,应将120百千克竹笋加工成笋干,最大利润为228000元


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和图形
和图形![]() ,给出如下定义:若图形
,给出如下定义:若图形![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 是边长为2的等边三角形,则称点
是边长为2的等边三角形,则称点![]() 是图形
是图形![]() 的一个“和谐点”.
的一个“和谐点”.
已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 的半径为
的半径为![]() .
.
(1)若![]() ,在点
,在点![]() 中,直线
中,直线![]() 的和谐点是___________;
的和谐点是___________;
(2)若![]() 上恰好存在2个直线
上恰好存在2个直线![]() 的和谐点,求
的和谐点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,线段
,线段![]() 上存在
上存在![]() 的和谐点,直接写出
的和谐点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
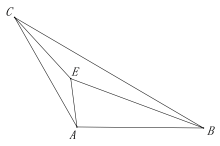
【题目】如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC 内一点,且满足![]() 则点E 在运动过程中所形成的图形的长为 ( )
则点E 在运动过程中所形成的图形的长为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州融创乐园是国内首个以南越文化、岭南风格为主题的游乐园,自2019年6月开园以来受到了国内外游客的热捧.某旅游团组织一批游客游玩了乐园内的四个网红项目,“A.双龙飞舞”、“B.飞跃广东”、“C.云霄塔”、“D.怒海狂涛”,并进行了“我最喜欢的一个项目”的投票评选活动,投票结果绘制成以下两幅尚未完整的统计图.请你根据图中提供的信息,解答下列问题:
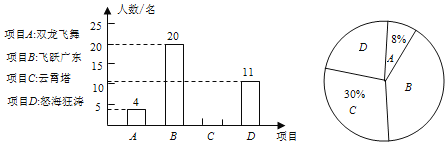
(1)参与投票的游客总人数为 人;
(2)扇形统计图中B所对的圆心角度数为 度,并补全条形统计图;
(3)从投票给“双龙飞舞“的3名男生和1名女生中随机抽取2名了解情况,请你用列举法求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
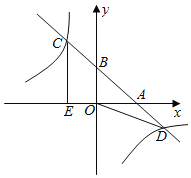
【题目】如图,直线y=﹣x+b与x、y轴的正半轴交于点A,B,与双曲线y=﹣![]() 交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() =
=![]() ,则b的值为_____.
,则b的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.
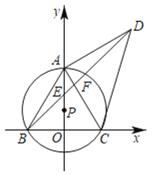
(1)求证:AB=AD;
(2)若BF=4,DF=6,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com