
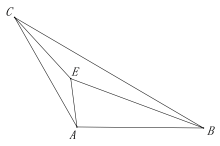
【题目】如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC 内一点,且满足![]() 则点E 在运动过程中所形成的图形的长为 ( )
则点E 在运动过程中所形成的图形的长为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
如图,将△AEC绕点A顺时针旋转120°得到△AFB,首先证明∠AFB=120°,推出E的轨迹为圆,进而可通过弧长计算出结果.
解:将△AEC绕点A顺时针旋转120°,使得AC与AB重合,得到△AFB,连接EF,过点A作AM⊥EF,过点O作ON⊥AC

由旋转可知:AE=AF,∠EAF=120°BF=CE
∴∠AEF=∠AFE=30°
∴在Rt△AEM中,EM=![]() ;在Rt△AFM中,MF=
;在Rt△AFM中,MF=![]()
∴EF=![]() ,即
,即![]()
∵![]()
∴![]()
∴∠EFB=90°
∴∠AFB=120°,
则∠AEC=120°为定角所对AC=3为定长
又因为点E在△ABC内部,
所以E的轨迹为弧GA的长度
当点E在G点时,∠CGA=120°
∴∠GOA=60°
∴在Rt△OAN中,![]()
∴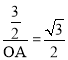 ,解得
,解得![]()
所以E的轨迹长为![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】“垃圾分类就是新时尚”.树立正确的垃圾分类观念,促进青少年养成良好的文明习惯,对于增强公共意识,提升文明素质具有重要意义.为了调査学生对垃圾分类知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制,单位:分),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息.
a.甲、乙两校学生样本成绩频数分布表及扇形统计图如下:
甲校学生样本成绩频数分布表(表1)
成绩m(分) | 频数 | 频率 |
|
| 0.10 |
|
|
|
| 4 | 0.20 |
| 7 | 0.35 |
| 2 |
|
合计 | 20 | 1.0 |

b.甲、乙两校学生样本成绩的平均分、中位数、众数、方差如下表所示:(表2)
学校 | 中位数 | 众数 | 方差 | |
甲 | 76.7 | 77 | 89 | 150.2 |
乙 | 78.1 | 80 |
| 135.3 |
其中,乙校20名学生样本成绩的数据如下:
54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91
请根据所给信息,解答下列问题:
(1)表1中![]() ___________;表2中的众数
___________;表2中的众数![]() _________;
_________;
(2)乙校学生样本成绩扇形统计图(图1)中,![]() 这一组成绩所在扇形的圆心角度数是_________度;
这一组成绩所在扇形的圆心角度数是_________度;
(3)在此次测试中,某学生的成绩是79分,在他所属学校排在前10名,由表中数据可知该学生是________校的学生(填“甲”或“乙”),理由是________________________;
(4)若乙校1000名学生都参加此次测试,成绩80分及以上为优秀,请估计乙校成绩优秀的学生约为________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
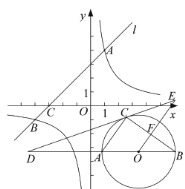
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知
,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知![]() .
.
(1)求证:AD是⊙O的切线;
(2)若BC=8,![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年的新冠疫情爆发,使很多农作物积压没法正常销售。为解决农民的困难,我市某食品加工公司主动分两次采购了一批竹笋, 第一次花费40万元,第二次花费60万元。已知第一次采购时每百千克竹笋的价格比去年的平均价格上涨了500元,第二次采购时每百千克竹笋的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每百千克竹笋的平均价格是多少元;
(2)该公司可将竹笋加工成笋干或罐头(湿笋),若单独加工成笋干,每天可加工8百千克竹笋,每百千克竹笋获利1000元; 若单独加工成罐头,每天可加工12百千克竹笋,每百千克竹笋获利600元,由于市场需要,所有采购的竹笋必需在30天内加工完毕,且加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,为获得最大利润,应将多少百千克竹笋加工成笋干?最大利润为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
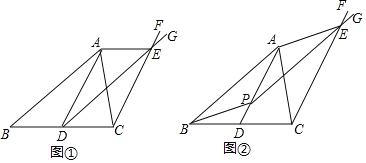
【题目】如图,AD是△ABC的中线,过点C作直线CF∥AD.
(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.
(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.
(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现![]() 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.
是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com