
【题目】如图,![]() 中,
中,![]() ,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知
,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知![]() .
.
(1)求证:AD是⊙O的切线;
(2)若BC=8,![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图(见解析),连接OD,先根据等腰三角形的性质可得![]() ,从而可得
,从而可得![]() ,再根据直角三角形的性质可得
,再根据直角三角形的性质可得![]() ,从而可得
,从而可得![]() ,然后根据等量代理可得
,然后根据等量代理可得![]() ,从而可得
,从而可得![]() ,最后根据圆的切线的判定即可得证;
,最后根据圆的切线的判定即可得证;
(2)先在![]() 中,利用正切三角函数值可求出AC的长,从而利用勾股定理可求出AB的长,再在
中,利用正切三角函数值可求出AC的长,从而利用勾股定理可求出AB的长,再在![]() 中,利用正切三角函数值可求出CD的长,从而利用勾股定理可求出AD的长,然后设⊙O的半径为
中,利用正切三角函数值可求出CD的长,从而利用勾股定理可求出AD的长,然后设⊙O的半径为![]() ,在
,在![]() 中,利用勾股定理即可得.
中,利用勾股定理即可得.
(1)如图,连接OD
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]() ,即
,即![]()
![]() 是圆O的半径
是圆O的半径
![]() 是⊙O的切线;
是⊙O的切线;
(2)![]()
![]()
在![]() 中,
中,![]() ,
,![]() ,即
,即![]()
解得![]()
由勾股定理得:![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
由勾股定理得:![]()
设⊙O的半径为![]() ,则
,则![]() ,
,![]()
由(1)可知,![]()
![]() 是直角三角形
是直角三角形
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
即![]()
解得![]()
即⊙O的半径为![]() .
.



 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个 | 20 | 50 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
合格数量m/个 | 19 | 46 | 93 | 185 | 459 | 922 | 1840 | 4595 | 9213 |
口罩合格率 | 0.950 | 0.920 | 0.930 | 0.925 | 0.918 | 0.922 | 0.920 | 0.919 | 0.921 |
下面四个推断合理的是( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921;
B.由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920;
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920;
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边均和一条对角线相等的四边形叫做邻和四边形.
(1)如图1,四边形ABCD中,∠ABC=70°,∠BAC=40°,∠ACD=∠ADC=80°,求证:四边形ABCD是邻和四边形.
(2)如图2,是由50个小正三角形组成的网格,每个小正三角形的顶点称为格点,已知A,B,C三点的位置如图,请在网格图中标出所有的格点D,使得以A,B,C,D为顶点的四边形为邻和四边形.
(3)如图3,△ABC中,∠ABC=90°,AB=4,BC=4![]() ,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),请你直接写出BM、DN和MN的数量关系:__________.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请写出直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以1个单位每秒的速度匀速运动,同时点
以1个单位每秒的速度匀速运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴正方向以2个单位每秒的速度匀速运动.
轴正方向以2个单位每秒的速度匀速运动.![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .当点
.当点![]() 到达点
到达点![]() 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为![]() 秒.在整个运动过程中,设
秒.在整个运动过程中,设![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() .
.
(1)求当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 、
、![]() 在同一直线上;
在同一直线上;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在图(3)中画出![]() 关于
关于![]() 的函数图象,直接写出
的函数图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=120°,AB=AC=3,点E是三角形ABC 内一点,且满足![]() 则点E 在运动过程中所形成的图形的长为 ( )
则点E 在运动过程中所形成的图形的长为 ( )
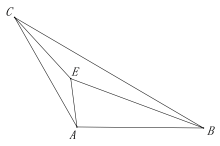
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为6的正方形ABCD,动点P、Q各从点A,D同时出发,分别沿边AD,DC方向运动,且速度均为每秒1个单位长度.
(1)AQ与BP关系为________________;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,试探究∠CEQ和∠BCE满足怎样的数量关系;
(3)如图3,将正方形变为菱形且∠BAD=60°,其余条件不变,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=![]() ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
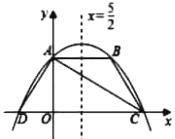
A.点B坐标为(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小腾的爸爸计划将一笔资金用于不超过10天的短期投资,针对这笔资金,银行专属客户经理提供了三种投资方案,这三种方案的回报如下:
方案一:每一天回报30元;
方案二:第一天回报8元,以后每一天比前一天多回报8元;
方案三:第一天回报0.5元,以后每一天的回报是前一天的2倍.
下面是小腾帮助爸爸选择方案的探究过程,请补充完整:
(1)确定不同天数所得回报金额(不足一天按一天计算),如下表:
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中![]() ________;
________;
(2)计算累计回报金额,设投资天数为![]() (单位:天),所得累计回报金额是
(单位:天),所得累计回报金额是![]() (单位:元),于是得到三种方案的累计回报金额
(单位:元),于是得到三种方案的累计回报金额![]() ,
,![]() ,
,![]() 与投资天数
与投资天数![]() 的几组对应值:
的几组对应值:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中![]() ________;
________;
(3)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,
,![]() ,并画出
,并画出![]() ,
,![]() ,
,![]() 的图象;
的图象;
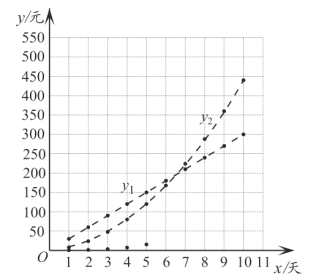
注:为了便于分析,用虚线连接离散的点.
(4)结合图象,小腾给出了依据不同的天数而选择对应方案的建议:
_________________________________________________________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com