
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У���![]() ����
����![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��1����λÿ����ٶ������˶���ͬʱ��
��1����λÿ����ٶ������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ����������2����λÿ����ٶ������˶���
����������2����λÿ����ٶ������˶���![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ������
������![]() �����
�����![]() ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ
ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ![]() �룮�������˶������У���
�룮�������˶������У���![]() ��
��![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ![]() ��
��
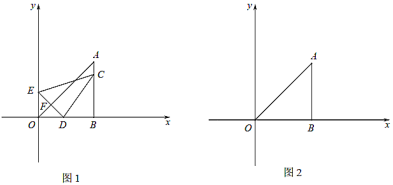
��1����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���
���![]() ��
��![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�
��2����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����ͼ��3���л���![]() ����
����![]() �ĺ���ͼ��ֱ��д��
�ĺ���ͼ��ֱ��д��![]() �����ֵ��
�����ֵ��
���𰸡���1��4����2�� ����3�����������
����3�����������![]() �����ֵ����8��
�����ֵ����8��
��������
��1����ͼ1��������![]() ���
���![]() ��
��![]() ��ͬһֱ����ʱ���ɵ�
��ͬһֱ����ʱ���ɵ�![]() �ǵ���ֱ�������Σ�����
�ǵ���ֱ�������Σ�����![]() ���������t�ķ��̣��ⷽ�̼��ɣ�
���������t�ķ��̣��ⷽ�̼��ɣ�
��2���������������G����Ϊ![]() ����Ϊ
����Ϊ![]() ��������������ۣ����ø�����������ϵʽ��
��������������ۣ����ø�����������ϵʽ��
��3����������ͼ����ͼ�����ֱ��д��![]() �����ֵ����8��
�����ֵ����8��
�⣺��1���ɵ�![]() ����
����![]() �á�OABΪ����ֱ�������Σ�
�á�OABΪ����ֱ�������Σ�
��![]()
��![]()
��![]() ���ǵ���ֱ�������Σ�
���ǵ���ֱ�������Σ�
��ͼ������![]() ���
���![]() ��
��![]() ��ͬһֱ����ʱ��
��ͬһֱ����ʱ��
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��![]() ��
��
��6-t=2t-6��
��t=4��

��2����![]() ��
�У�![]() ,
,
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��OE=OD=2t��
![]()
![]()
��![]()
��![]() ,
,
���G����Ϊ![]()
��ͼ2����![]() ʱ
ʱ
![]()
![]()
=![]() ��
��

��ͼ3��![]() ʱ��
ʱ��
![]()
![]()
=![]() ��
��

��ͼ4����![]() ʱ��
ʱ��
![]()
![]()

��
��3����ͼ���ɺ���ͼ���![]() �����ֵ����8��
�����ֵ����8��



 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��Ƹ��ѧ��ʦ��������Ƹ����רҵ���ܲ��ԺͿ��ý�ѧչʾ������Ŀ�Ŀ��ˣ�������˵����־�Ϊ100�֣�ѧУ����������Ŀ�ĵ÷ְ�һ���ı���������ܳɼ�����ͳ�ƣ��μӿ��˵�4��������������Ŀ�ĵ÷����£�

��1���������㣬1�ſ������ܳɼ�Ϊ78�֣���רҵ���ܲ��Ե÷ֺͿ��ý�ѧչʾ�÷ֱַ�ռ�ܳɼ��İٷֱȣ�
��2����ѧУ¼ȡ�ܳɼ���ߵĿ�����ͨ������˵����4����������һ�������ᱻ¼ȡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
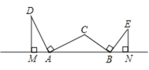
����Ŀ����ͼ���ڡ�ABC �У���ACB Ϊ�۽ǣ��� AC �Ƶ� A ����ʱ�뷽����ת 90���õ�AD���� BC �Ƶ� B ��˳ʱ�뷽����ת 90���õ� BE���� DM��AB �ڵ� M��EN��AB�� �� N�� �� AB��10��EN��4�� �� DM��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
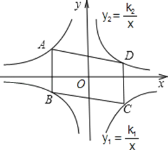
����Ŀ����ͼ��ƽ���ı���ABCD�Ķ���ΪA��C��˫����y1=![]() �ϣ�B��D��˫����
�ϣ�B��D��˫����![]() �ϣ�k1=2k2��k1��0����AB��y�ᣬ
�ϣ�k1=2k2��k1��0����AB��y�ᣬ![]() =24����k2��ֵΪ�� ��
=24����k2��ֵΪ�� ��
A.4B.��4C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABOC�Ķ���O������ԭ�㣬��BO��x��ĸ������ϣ�![]() ������C������Ϊ
������C������Ϊ![]() ��x����������
��x����������![]() ��ͼ�������ζԽ���AO���ڵ�D������BD����
��ͼ�������ζԽ���AO���ڵ�D������BD����![]() ��ʱ��k��ֵ��______��
��ʱ��k��ֵ��______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() ����O��б��AB�ϣ���OΪԲ�ģ�OB��Ϊ�뾶����O����BC���ڵ�D������AD����֪
����O��б��AB�ϣ���OΪԲ�ģ�OB��Ϊ�뾶����O����BC���ڵ�D������AD����֪![]() ��
��
��1����֤��AD�ǡ�O�����ߣ�
��2����BC=8��![]() �����O�İ뾶��
�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶��ʦ���Ծ���������ѧ���������Ⱥ�Ƚ������۵��飬��������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ������������ѧ���IJ����������������ͼ������������ͳ��ͼ�������ͼ��������Ϣ����������⣺
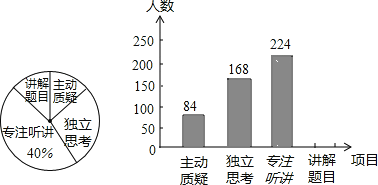
��1������������У�һ��������� ����ѧ����
��2���뽫����ͳ��ͼ����������
��3�����ȫ����12000������ѧ������ô���Ծ��������У�����˼����ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
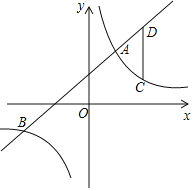
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��kx+b��k��0���뷴��������y��![]() ��m��0����ͼ���ཻ��A(2��4)��B(n����2)���㣮
��m��0����ͼ���ཻ��A(2��4)��B(n����2)���㣮
��1����һ�κ����ͷ����������ı���ʽ��
��2����C�ǵ�һ�����ڷ���������ͼ���ϵ�һ�㣬�ҵ�C��A���Ҳ࣬����C��CDƽ����y�ύֱ��AB�ڵ�D������CΪԲ�ģ�CD��Ϊ�뾶�ġ�Cǡ����y�����У����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() Ϊ�Ż�
Ϊ�Ż�![]() �ϵĶ��㣨�����
�ϵĶ��㣨�����![]() ��
��![]() �غϣ����ڵ�
�غϣ����ڵ�![]() �˶��Ĺ����У����½�����ȷ���ǣ� ��
�˶��Ĺ����У����½�����ȷ���ǣ� ��

A.![]() �Ĵ�С�ı�B.��
�Ĵ�С�ı�B.��![]() ����
����![]() ����ֱ�ߵľ���������ֵ
����ֱ�ߵľ���������ֵ
C.�߶�![]() ��
��![]() �ij���֮�Ͳ���D.ͼ����Ӱ���ֵ��������
�ij���֮�Ͳ���D.ͼ����Ӱ���ֵ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com