
����Ŀ��ijѧУ��Ƹ��ѧ��ʦ��������Ƹ����רҵ���ܲ��ԺͿ��ý�ѧչʾ������Ŀ�Ŀ��ˣ�������˵����־�Ϊ100�֣�ѧУ����������Ŀ�ĵ÷ְ�һ���ı���������ܳɼ�����ͳ�ƣ��μӿ��˵�4��������������Ŀ�ĵ÷����£�

��1���������㣬1�ſ������ܳɼ�Ϊ78�֣���רҵ���ܲ��Ե÷ֺͿ��ý�ѧչʾ�÷ֱַ�ռ�ܳɼ��İٷֱȣ�
��2����ѧУ¼ȡ�ܳɼ���ߵĿ�����ͨ������˵����4����������һ�������ᱻ¼ȡ��
���𰸡���1��רҵ���ܲ��Ե÷ֺͿ��ý�ѧչʾ�÷ֱַ�ռ�ܳɼ��İٷֱȷֱ�Ϊ40%��60%����2��3�ſ���
��������
��1������רҵ���ܱ��Ե÷�ռ�ܳɼ��İٷֱ���![]() ������1�ſ������ܳɼ�Ϊ78���г�������⼴�ɣ�
������1�ſ������ܳɼ�Ϊ78���г�������⼴�ɣ�
��2�����ݼ�Ȩƽ������ʽ�ֱ����4�������ܳɼ����ٱȽϴ�С������⣮
�⣺��1����רҵ���ܲ��Ե÷�ռ�ܳɼ��İٷֱ���a��
�������⣬��90a+70(1-a)=78��
��������̣���a=40%��
1-40%=60%��
����רҵ���ܲ��Ե÷ֺͿ��ý�ѧչʾ�÷�ռ�ܳɼ��İٷֱȷֱ���40%��60%��
��2��2�ſ����ܳɼ�Ϊ70��0.4+90��0.6=82���֣�
3�ſ����ܳɼ�Ϊ86��0.4+80��0.6=82.4���֣�
4�ſ����ܳɼ�Ϊ75��0.4+86��0.6=81.6���֣�
��Ϊ82.4��82��81.6��78������3�ſ����ᱻ¼ȡ��


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
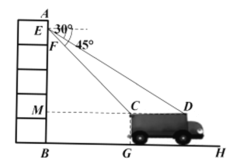
����Ŀ���¹�״�������鱬���������人��Ҫ������Ԯ���ʣ���ͼС��վ��һ��������¥![]() �ĵ���㣨ÿ��߶���ȣ����۾�����¥����ľ���
�ĵ���㣨ÿ��߶���ȣ����۾�����¥����ľ���![]() m��������¥����ͣ��һ��װ�ؾ�Ԯ���ʵĻ���������β��C�㵽¥���ˮƽ����
m��������¥����ͣ��һ��װ�ؾ�Ԯ���ʵĻ���������β��C�㵽¥���ˮƽ����![]() m�����䶥��C�������Ĵ�ֱ����
m�����䶥��C�������Ĵ�ֱ����![]() m����E����C��ĸ���Ϊ
m����E����C��ĸ���Ϊ![]() �����D��ĸ���Ϊ
�����D��ĸ���Ϊ![]() ����С������¥��
����С������¥��![]() �ĸ߶Ⱥͻ�������
�ĸ߶Ⱥͻ�������![]() �ij��ȣ��������С�����һλ����
�ij��ȣ��������С�����һλ����
���ο����ݣ�![]() ��
��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������

A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
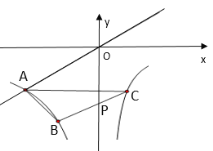
����Ŀ����ͼ����֪˫����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��˫����
��˫����![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() ����ƽ����˫����
����ƽ����˫����![]() ���ڵ�
���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����˫����
����˫����![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ������
������![]() ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD��������ȫ�Ⱦ���ƴ�ɵģ�AC��DE��EF��FG��HG��HB�ֱ��ڵ�P��Q��K��M��N������EPQ����GKM����BNC���������ΪS1��S2��S3����S1+S3=30����S2��ֵΪ�� ����
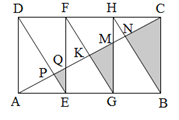
A.6B.8
C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¹����鷢��������Ϊ��֤�����ڼ�Ŀ��ֹ�Ӧ��ij��˾�ӽ�ת��������������������ֶ�����ƿ��֣������ת��ʱ��İ��������ʽͶ�������վ�����100������ֵIJ��ܣ�����Ч�ʸߣ����ҿ����ͼ�ϸ���Ҳ��������������������������ٶ������������ʼ�ֶ�һ�����ֽ�����������������ݣ�ͳ�����£�
�������n/�� | 20 | 50 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
�ϸ�����m/�� | 19 | 46 | 93 | 185 | 459 | 922 | 1840 | 4595 | 9213 |
���ֺϸ��� | 0.950 | 0.920 | 0.930 | 0.925 | 0.918 | 0.922 | 0.920 | 0.919 | 0.921 |
�����ĸ��ƶϺ������ǣ� ��
A.�������ֵ�������10000��ʱ�����ֺϸ��������9213�����������������������ֺϸ����ĸ�����0.921��
B.���ڳ����ֵ������ֱ���50��2000��ʱ�����ֺϸ��ʾ���0.920�����Կ��Թ������������������ֺϸ����ĸ�����0.920��
C.���ų�����������ӣ������ֺϸ�����Ƶ������0.920�����ڶ�����ʾ��һ�����ȶ��ԣ����Կ��Թ������������������ֺϸ����ĸ�����0.920��
D.�������ֵ������ﵽ20000��ʱ�������ֺϸ����ĸ���һ����0.921��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ![]() ����ֱ��
����ֱ��![]() ��y������ƽ��3����λ���Ⱥ�ǡ�þ���B��C���㣮
��y������ƽ��3����λ���Ⱥ�ǡ�þ���B��C���㣮
��1����k��ֵ�͵�C�����ꣻ
��2����������![]() �ı���ʽ������D�����ꣻ
�ı���ʽ������D�����ꣻ
��3����֪��E�ǵ�D����ԭ��ĶԳƵ㣬��������![]() ���߶�
���߶�![]() ǡ��һ�������㣬��Ϻ�����ͼ����a��ȡֵ��Χ��
ǡ��һ�������㣬��Ϻ�����ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪�����߶���C��1��4��������y�ύ�ڵ�D��0��3����
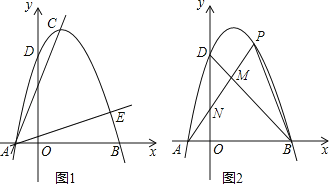
��1����������ߵĽ���ʽ������x��Ľ���A��B�����ꣻ
��2����ֱ��AC�Ƶ�A˳ʱ����ת45���õ�ֱ��AE���������ߵ���һ������ΪE���������E�����ꣻ
��3����ͼ2����P�Ǹ���������λ�ڵ�һ���ĵ㣬�߶�AP��BD�ڵ�M����y���ڵ�N����BMP�͡�DMN������ֱ�ΪS1��S2����S1��S2�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У���![]() ����
����![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��1����λÿ����ٶ������˶���ͬʱ��
��1����λÿ����ٶ������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ����������2����λÿ����ٶ������˶���
����������2����λÿ����ٶ������˶���![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ������
������![]() �����
�����![]() ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ
ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ![]() �룮�������˶������У���
�룮�������˶������У���![]() ��
��![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ![]() ��
��
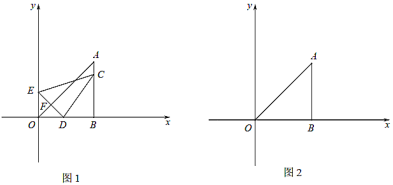
��1����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���
���![]() ��
��![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�
��2����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
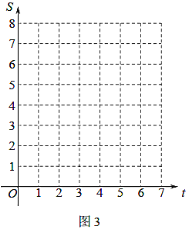
��3����ͼ��3���л���![]() ����
����![]() �ĺ���ͼ��ֱ��д��
�ĺ���ͼ��ֱ��д��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com