
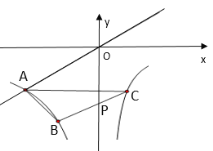
【题目】如图,已知双曲线![]() 和
和![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,将直线
,将直线![]() 向下平移与双曲线
向下平移与双曲线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,,则
,,则![]() 的值为__________.
的值为__________.
【答案】![]()
【解析】
连接OB,OC,作BE⊥OP于E,CF⊥OP于F,先证得S△OBC=S△ABC=6,由![]() ,得出S△OPB=4,S△OPC=2,根据反比例函数系数k的几何意义得出S△OBE=
,得出S△OPB=4,S△OPC=2,根据反比例函数系数k的几何意义得出S△OBE=![]() ,进一步得出S△PBE=S△OBE-S△OPB=6-4=2,再通过证得△BEP∽△CFP,得出S△CFP=
,进一步得出S△PBE=S△OBE-S△OPB=6-4=2,再通过证得△BEP∽△CFP,得出S△CFP=![]() ,然后根据S△OCF= S△OPC-S△CFP求得△OCF的面积为
,然后根据S△OCF= S△OPC-S△CFP求得△OCF的面积为![]() ,从而求得k的值.
,从而求得k的值.
如图,连接OB,OC,作BE⊥OP于E,CF⊥OP于F.
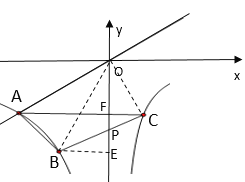
∵OA∥BC,
∴S△OBC=S△ABC=6
∵![]() ,
,
∴S△OPB=4,S△OPC=2,
又由反比例函数的几何意义可知![]() ,
,
∴![]() .
.
∵△BEP∽△CFP,
∴![]() ,
,
∴![]() ,
,
∴S△OCF= S△OPC-S△CFP=![]()
∴k=﹣3.
故答案为:﹣3.


科目:初中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)
频率分布表 | ||
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 10 | 0.20 |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | ||

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.

(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】远远在一个不透明的盒子里装了4个除颜色外其他都相同的小球,其中有3个是红球,1个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC内接于⊙O,AT切⊙O于点A,AB=BC,且AT∥BC.
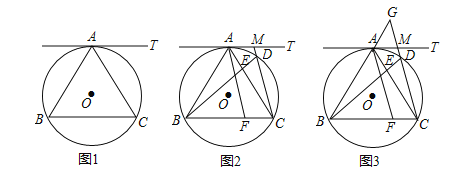
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点M在射线AT上,连接CM交⊙O于点D,连接BD交AC于点E,AF∥CM交BC于点F,求证:AE=CF;
(3)如图3,在(2)的条件下,延长BA、CM交于点G,若BD=40,CD=25,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品的进价为每件40元.现在的售价是每件60元.每星期可卖出300件.市场调查反映:如调整价格,每涨价一元.每星期要少卖出10件;每降价一元,每星期可多卖出18件.如何定价才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
扇形统计图
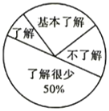
条形统计图

(1)接受问卷调查的学生共有_______人,扇形统计图中“不了解”部分所对应扇形的圆心角度数为_______,并把条形统计图补充完整;
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
(3)若从对校园安全知识达到“了解”程度的![]() ,
,![]() ,
,![]()
![]() 个女生和
个女生和![]() ,
,![]()
![]() 个男生中随机抽取
个男生中随机抽取![]() 人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到
人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到![]() 个男生和
个男生和![]() 个女生的概率.
个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴相交于点C(0,3),且
轴相交于点C(0,3),且![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
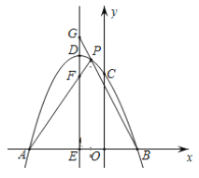
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)求抛物线的表达式.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() 、
、![]() 当点
当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com