
【题目】下面是小文设计的“过圆外一点作圆的切线”的作图过程.已知:![]() 和圆外一点
和圆外一点![]() .求作:过点
.求作:过点![]() 的
的![]() 的切线.作法:①连接
的切线.作法:①连接![]() ;②以
;②以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ;③作直线
;③作直线![]() ,
,![]() ;所以直线
;所以直线![]() ,
,![]() 为
为![]() 的切线.
的切线.
根据小文设计的作图过程,完成下面的证明.
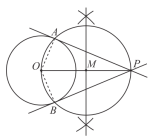
证明:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,
的直径,
∴![]() =∠________=________
=∠________=________
(________)(填推理的依据).
∴![]() ,________
,________![]() .
.
∵![]() ,
,![]() 为
为
∴直线![]() ,
,![]() 为
为![]() 的切线(________)(填推理的依据).
的切线(________)(填推理的依据).
 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与x、y轴的正半轴交于点A,B,与双曲线y=﹣![]() 交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() =
=![]() ,则b的值为_____.
,则b的值为_____.
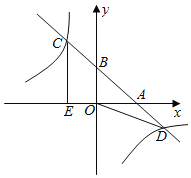
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
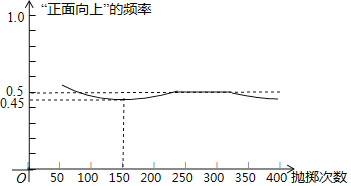
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
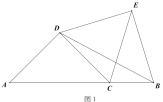
【题目】点C为线段![]() 上一点,以
上一点,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,在
,在![]() 外侧,以
外侧,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() .
.
(1)如图1,当![]() 时:
时:
①求证:![]() ;
;
②判断线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
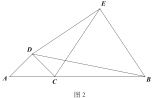
(2)如图2,当![]() 时,
时,![]() 与
与![]() 的数量关系是否保持不变?
的数量关系是否保持不变?
对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:
想法1:尝试将点D为旋转中心,过点D作线段![]() 垂线,交
垂线,交![]() 延长线于点G,连接
延长线于点G,连接![]() ;通过证明
;通过证明![]() 解决以上问题;
解决以上问题;
想法2:尝试将点D为旋转中心,过点D作线段![]() 垂线,垂足为点G,连接
垂线,垂足为点G,连接![]() .通过证明
.通过证明![]() 解决以上问题;
解决以上问题;
想法3:尝试利用四点共圆,过点D作![]() 垂线段
垂线段![]() ,连接
,连接![]() ,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
请你参考上面的想法,证明![]() (一种方法即可).
(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过直线外一点且与这条直线相切的圆称为这个点和这条直线的点线圆.特别地,半径最小的点线圆称为这个点和这条直线的最小点线圆.
在平面直角坐标系![]() 中,点
中,点![]() .
.
(1)已知点![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为圆心,1为半径作
为圆心,1为半径作![]() ,
,![]() ,以
,以![]() 为圆心,2为半径作
为圆心,2为半径作![]() ,其中是点
,其中是点![]() 和
和![]() 轴的点线圆的是________;
轴的点线圆的是________;
(2)记点![]() 和
和![]() 轴的点线圆为
轴的点线圆为![]() ,如果
,如果![]() 与直线
与直线![]() 没有公共点,求
没有公共点,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)直接写岀点![]() 和直线
和直线![]() 的最小点线圆的圆心的横坐标
的最小点线圆的圆心的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.
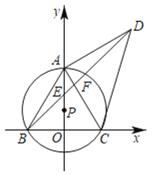
(1)求证:AB=AD;
(2)若BF=4,DF=6,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
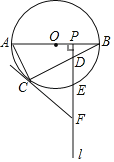
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,试证明四边形
,试证明四边形![]() 为菱形;
为菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2﹣4ax+a+1(a>0)
(1)若二次函数的图象与x轴有交点,求a的取值范围;
(2)若P(m,n)和Q(5,b)是抛物线上两点,且n>b,求实数m的取值范围;
(3)当m≤x≤m+2时,求y的最小值(用含a、m的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com