
【题目】将一大、一小两个等腰直角三角形拼在一起,![]() ,连接
,连接![]() .
.
(1)如图1,若![]() 三点在同一条直线上,则
三点在同一条直线上,则![]() 与
与![]() 的关系是 ;
的关系是 ;
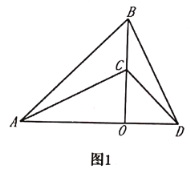
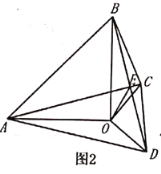
(2)如图2,若![]() 三点不在同一条直线上,
三点不在同一条直线上,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,猜想
,猜想![]() 之间的数量关系,并给予证明;
之间的数量关系,并给予证明;
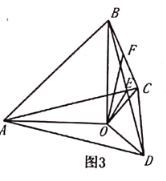
(3)如图3,在(2)的条件下作![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 与
与![]() 之间的关系.
之间的关系.
【答案】(1)![]() 且
且![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() 且
且![]() .
.
【解析】
(1)根据题意利用全等三角形的判定与性质以及延长AC交BD于点C’进行角的等量代换进行分析即可;
(2)根据题意在![]() 上截取
上截取![]() ,连接
,连接![]() ,并全等三角形的判定证明
,并全等三角形的判定证明![]() 和
和![]() ,进而利用勾股定理得出
,进而利用勾股定理得出![]() 进行分析求解即可;
进行分析求解即可;
(3)过点B作BM∥OC,交OF的延长线于点M,延长FO交AD于点N,证明BFMCFO,AODOBM,进而即可得到结论.
解:![]() ∵
∵![]() ,
,
∴![]() ,
,
延长AC交BD于点C’,如下图:
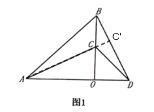
∵![]()
![]() ,
,
∴![]() ,
,
即![]() ,综上
,综上![]() 且
且![]() ,
,
故答案为:![]() 且
且![]() ;
;
![]()
证明:在![]() 上截取
上截取![]() ,连接
,连接![]()

![]()
![]()
![]()
在![]() 和
和![]() 中
中
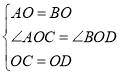
![]()
![]()
在![]() 和
和![]() 中
中
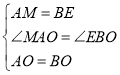
![]()
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
![]() ;
;
![]() 且
且![]() ,理由如下:
,理由如下:
过点B作BM∥OC,交OF的延长线于点M,延长FO交AD于点N,
∵BM∥OC,
∴∠M=∠FOC,
∵∠BFM=∠CFO,BF=CF,
∴BFMCFO(AAS),
∴OF=MF,BM=CO,
∵DO=CO,
∴DO=BM,
∵BM∥OC,
∴∠OBM+∠BOC=180°,
∵∠BOC+∠AOD=360°-90°-90°=180°,
∴∠OBM=∠AOD,
又∵AO=BO,
∴AODOBM(SAS),
∴AD=OM=2OF ,∠BOM=∠OAD,
∵∠BOM+∠AON=180°-90°=90°,
∴∠OAD+∠AON=90°,即OF⊥AD.
∴![]() 且
且![]() .
.


科目:初中数学 来源: 题型:
【题目】古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)求证:CD是⊙O的切线;
(2)小明在研究的过程中发现![]() 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.
是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
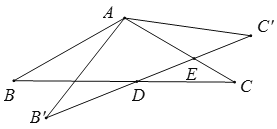
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.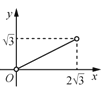 B.
B.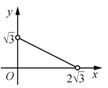 C.
C.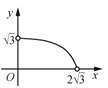 D.
D.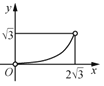
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒1个单位长度的速度运动,动点
以每秒1个单位长度的速度运动,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒2个单位长度的速度运动,过点
以每秒2个单位长度的速度运动,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .点
.点![]() 分别从点
分别从点![]() 同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为
同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为![]() 秒
秒![]() .
.
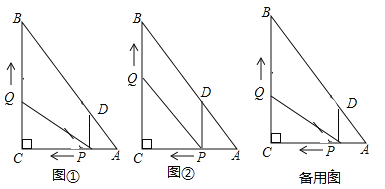
(1)如图①,直接用含![]() 的代数式分别表示:
的代数式分别表示:![]() ,
,![]() ______,
______,
(2)如图②,
①当![]() _____秒时,四边形
_____秒时,四边形![]() 为平行四边形.
为平行四边形.
②是否存在![]() 的值,使四边形
的值,使四边形![]() 为菱形?若存在,写出
为菱形?若存在,写出![]() 的值;若不存在,请求出当点
的值;若不存在,请求出当点![]() 的速度(匀速运动)变为每秒多少个单位长度时,才能使四边形
的速度(匀速运动)变为每秒多少个单位长度时,才能使四边形![]() 在某一时刻成为菱形?
在某一时刻成为菱形?
(3)设![]() 的外接圆面积为
的外接圆面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并判断当
的函数关系式,并判断当![]() 最小时,
最小时,![]() 的外接圆与直线
的外接圆与直线![]() 的位置关系,并且说明理由.
的位置关系,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 在平面直角坐标系
在平面直角坐标系![]() 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点
中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点![]() 的坐标是( )
的坐标是( )
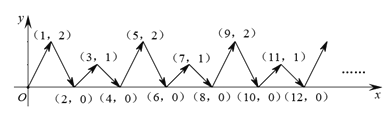
A.(26,0)B.(26,1)C.(27,1)D.(27,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)求点![]() 坐标;
坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 及抛物线在
及抛物线在![]() 两点之间的部分围成的封闭区域(不含边界)记为
两点之间的部分围成的封闭区域(不含边界)记为![]() .
.
①当![]() 时,结合函数图象,直接写出区域
时,结合函数图象,直接写出区域![]() 内的整点个数;
内的整点个数;
②如果区域![]() 内有2个整点,请求出
内有2个整点,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
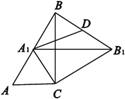
【题目】如图,RtΔABC中∠C=90°,∠ABC=30°,ΔABC绕点C顺时针旋转得ΔA1B1C,当A1落在AB上时,连接B1B,取B1B的中点D,连接A1D,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com