
分析 (1)原式第一项利用负指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=$\frac{9}{4}$-3$\sqrt{3}$+2$\sqrt{3}$-2+$\sqrt{3}$=$\frac{1}{4}$;
(2)原式=$\frac{x-1}{x}$•$\frac{x}{(x-1)^{2}}$=$\frac{1}{x-1}$,
当x=$\sqrt{2}$时,原式=$\sqrt{2}$+1.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
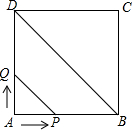 如图,正形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).
如图,正形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
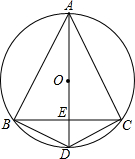 如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.
如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
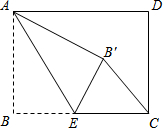 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 19.4×108 | B. | 1.94×108 | C. | 1.94×109 | D. | 19.4×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
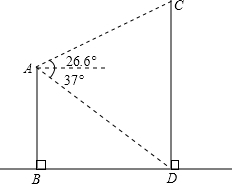 如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.
如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com