
分析 因为$\sqrt{432n}$是整数,且$\sqrt{432n}$=$\sqrt{{12}^{2}×3}$=12$\sqrt{3n}$,因为$\sqrt{3n}$是整数,则3n是完全平方数,可得n的最小值.
解答 解:∵$\sqrt{432n}$是整数,且$\sqrt{432n}$=$\sqrt{{12}^{2}×3}$=12$\sqrt{3n}$,
∵$\sqrt{3n}$是整数,
∴3n是完全平方数,满足条件的最小正整数n为3.
点评 此题主要考查了乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.二次根式的运算法则:乘法法则$\sqrt{a}$$•\sqrt{b}$=$\sqrt{ab}$,解题关键是分解成一个完全平方数和一个代数式的积的形式.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “a是任意实数,则a2≥0”是随机事件 | |
| B. | 某彩票的中奖率为1%,则买100张彩票一定有1张会中奖 | |
| C. | 若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为$\frac{1}{2}$ | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
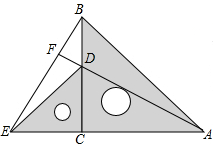 把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com