
����Ŀ��ijС��Ϊ���̻��������ƻ������ι���A��B���ֻ��ݣ���һ�ηֱ�A��B���ֻ���30�ú�15�ã�������675Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã�������265Ԫ�����ι�����A��B���ֻ��ݼ۸���ֱ���ͬ����
��1��A��B���ֻ���ÿ�õļ۸�ֱ��Ƕ���Ԫ��
��2��������A��B���ֻ��ݹ�31�ã���B�ֻ��ݵ���������A�ֻ��ݵ�������2�����������һ�ַ�����ʡ�ķ�����������÷���������ã�
���𰸡�
��1���⣺��A�ֻ���ÿ�õļ۸�xԪ��B�ֻ���ÿ�õļ۸�yԪ����������ã� ![]() ��
��
��ã� ![]() ��
��
��A�ֻ���ÿ�õļ۸���20Ԫ��B�ֻ���ÿ�õļ۸���5Ԫ
��2���⣺��A�ֻ��ݵ�����Ϊm�ã���B�ֻ��ݵ�����Ϊ��31��m���ã�
��B�ֻ��ݵ���������A�ֻ��ݵ�������2����
��31��m��2m��
��ã�m�� ![]() ��
��
��m����������
��m��Сֵ=11��
�蹺�������ܷ���ΪW=20m+5��31��m��=15m+155��
��k��0��
��W��x�ļ�С����С��
��m=11ʱ��W��Сֵ=15��11+155=320��Ԫ����
�𣺹���A�ֻ��ݵ�����Ϊ11�á�B��20�ã�������ʡ����ʡ������320Ԫ
����������1��ץס��֪��֪������ϵ�ǣ���һ�ηֱ�A��B���ֻ���30�ú�15�ã�������675Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã�������265Ԫ����δ֪���������̣���⼴�ɡ�
��2�����ⲻ�ȹ�ϵ�ǣ�B�ֻ��ݵ�������A�ֻ��ݵ�������2����������ϵ��A�ֻ��ݵ�����+B�ֻ��ݵ�����=31���в���ʽ�������m��ȡֵ��Χ����������������ܷ���ΪW��m�ĺ�������ʽ������m��ȡֵ��Χ�����ʡ�ķ�����


 �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��һ������x1��x2��x3��x4��x5��ƽ������2��������![]() ����ô��һ������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ�����ͷ���ֱ��ǣ�������
����ô��һ������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ�����ͷ���ֱ��ǣ�������
A. 2��![]() B. 2��1 C. 4��
B. 2��1 C. 4��![]() D. 4��3
D. 4��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�����õ���A��B��C������BB'������A��B��B=20�������A�Ķ�����_____��
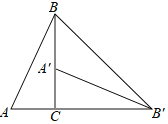
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�����оٰ����조������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 8 |
��3�� | 35��x��40 | 16 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺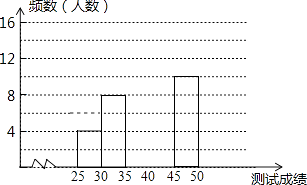
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�
��4����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㲹ȫ֤�����̣���ͼ��DG��BC��AC��BC��EF��AB����1=��2����֤��EF��CD

֤������DG��BC��AC��BC(��֪)
���DGB=90�㣬��ACB=90��٣� ��
���DGB=��ACB ��( )
��DG��AC ��( )
���2= ��________ �ݣ� ��
�֡�1=��2 �ޣ� ��
���1=��DCA �ߣ� ��
��EF��CD �ࣨ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽ��������A��B�����й�·����·��������ҹ�����A�ع���һ��ÿ��1000Ԫ��ԭ�Ͼ���·120km��·10km�˻ع������Ƴ�ÿ��8000Ԫ�IJ�Ʒ����·110km��·20km���۵�B�أ���֪��·���˼�Ϊ1.2Ԫ/���֡�ǧ��)����·���˼�Ϊ1.5Ԫ/(�֡�ǧ��)�������������乲֧����·�˷�124800Ԫ����·�˷�19500Ԫ��
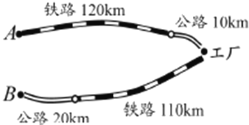
��1����ԭ����x�֣���Ʒ��y�֣���������������ϵ��д�±�
ԭ��x�� | ��Ʒy�� | �ϼƣ�Ԫ�� | |
��·�˷� | 124800 | ||
��·�˷� | 19500 |
�����ϱ��з�������ԭ�ϺͲ�Ʒ��������
��2��������Ʒ�����ۿ��ԭ�Ϸ�������ѵĺͶ����Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����
��̽���뷢�֣�
��һ����ѧ̽����У���ѧ��ȤС��ͨ��̽�����ֿ���ͨ�����������IJ�������ʾ�������������ľ�������ͼ1�������߶εij��ȿɱ�ʾΪ��AB=4-2=2��CB=4-(-2)=6��DC=-2-(-4)=2�������ۣ����������������ʾ����Ϊ�ֱ�a��b(b��a)�������������ľ���Ϊb-a(�����ýϴ������ȥ��С����)

�����������ã�
(1)��ͼ2��������E��F�����ʾ�����ֱ�Ϊ-2��-5���Լ��㣺EF=______��AF=______��
(2)�������Ϸֱ���������M��N��H����������M��ʾ����Ϊ-18����N��ʾ����Ϊ2018����֪��HΪ�߶�MN�е㣬����H��ʾ����m���������m��ֵ��
����չ�����죩
(3)��ͼ3����A��ʾ��x����B��ʾ-1����C��ʾ3x+8����AB=![]() BC�����A�͵�C�ֱ��ʾʲô����
BC�����A�͵�C�ֱ��ʾʲô����
(4)��(3)�����£���ͼ3���������Ƿ�������������ĵ�D��ʹDA+DC=3DB�������ڣ���ֱ��д����D��ʾ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����ADB=��CBD����������һ���������Բ����ж��ı���ABCD��ƽ���ı��ε��ǣ� ��
A����ABD=��CDB
B����DAB=��BCD
C����ABC=��CDA
D����DAC=��BCA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��¥�Ķ�����һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60�㣮������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪sin��BAH= ![]() ��AB=10�ף�AE=15�ף�
��AB=10�ף�AE=15�ף�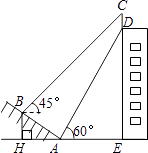
��1�����B��ˮƽ��AE�ĸ߶�BH��
��2��������CD�ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com