
【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH= ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.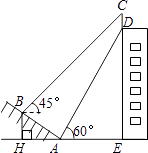
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
【答案】
(1)解:由题意得,sin∠BAH= ![]() =
= ![]() ,又AB=10米,
,又AB=10米,
∴BH= ![]() AB=5米
AB=5米
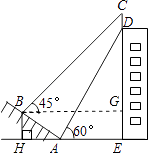
(2)解:∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=5,AH=5 ![]() ,
,
∴BG=AH+AE=5 ![]() +15,
+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5 ![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE= ![]() AE=15
AE=15 ![]() .
.
∴CD=CG+GE﹣DE=5 ![]() +15+5﹣15
+15+5﹣15 ![]() =20﹣10
=20﹣10 ![]() .
.
答:广告牌CD的高度为(20﹣10 ![]() )米.
)米.
【解析】(1)根据正弦的概念求出BH的长;(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE﹣DE即可求出广告牌的高度.
【考点精析】认真审题,首先需要了解关于仰角俯角问题(仰角:视线在水平线上方的角;俯角:视线在水平线下方的角).


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A,B两种花草,第一次分别购进A,B两种花草30棵和15棵,共花费675元;第二次分别购进A,B两种花草12棵和5棵,共花费265元(两次购进的A、B两种花草价格均分别相同).
(1)A,B两种花草每棵的价格分别是多少元?
(2)若购买A,B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你设计一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
(2)如图(1),设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值.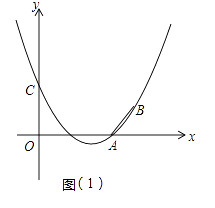
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用-5、-2、1,三个数按照给出顺序构造一组无限循环数据。
(1)求第2018个数是多少?
(2)求前50个数的和是多少?
(3)试用含![]() (
(![]() 为正整数)的式子表示出数“-2所在的位置数;
为正整数)的式子表示出数“-2所在的位置数;
(4)请你算出第![]() 个,第
个,第![]() 个,第
个,第![]() 个这三个数的和?
个这三个数的和?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com