
【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH= ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.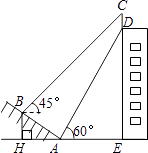
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC为⊙O的内接三角形,点G和点F在⊙O上且位于点A的两侧,连接BF、CG交于点E,且BF=CG.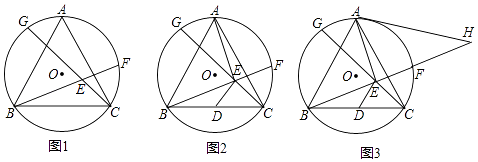
(1)求证:∠BEC=120°;
(2)如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;
(3)如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2, 0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )

A.(2,0)B.(-1,-1)C.( -2,1)D.(-1, 1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 . 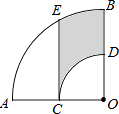
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
, OA=10,E为x轴负半轴上一点,且tan∠AOE= ![]() .
.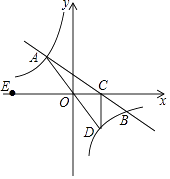
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一蓄水池中有水40m3,如果每分钟放出2m3的水,水池里的水量与放水时间有如下关系:
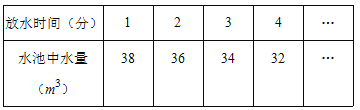
下列数据中满足此表格的是( )
A. 放水时间8分钟,水池中水量25m3
B. 放水时问20分钟,水池中水量4m3
C. 放水时间26分钟,水池中水量14m3
D. 放水时间18分钟,水池中水量4m3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com