
【题目】如图1,等边△ABC为⊙O的内接三角形,点G和点F在⊙O上且位于点A的两侧,连接BF、CG交于点E,且BF=CG.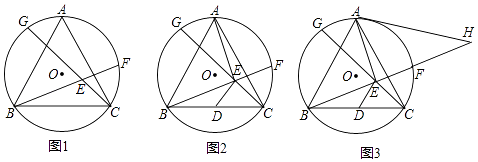
(1)求证:∠BEC=120°;
(2)如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;
(3)如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长.
【答案】
(1)证明:如图1中,
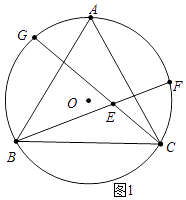
∵BF=CG,
∴ ![]() =
= ![]()
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴∠ACG=∠CBF,
∵∠GEB=∠FBC+∠ECB=∠ACE+∠ECB=60°,
∴∠BEC=180°﹣∠GEB=120°.
(2)证明:如图2中,连接BG、AG、CF、AF、GF,GF与AE交于点M.
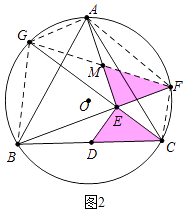
∵∠BEC=120°,
∴∠FEC=∠GEB=60°,
∵∠BGE=∠BAC=60°,∠EFC=∠BAC=60°,
∴△BGE,△EFC都是等边三角形,
∵∠AFB=∠ACB=60°,
∴∠GEB=∠AFB=60°,
∴GE∥AF,同理BF∥AG,
∴四边形AGEF是平行四边形,
∴GM=MF,AM=ME,
∵∠GBF=∠BAC=60°,
∴ ![]() =
= ![]() ,
,
∵BD=CD,
∴MF=CD,
在△MFE和△DCE中,
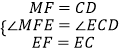 ,
,
∴△MFE≌△DCE,
∴ME=DE,
∴AE=2DE.
(3)解:如图3中,在图(2)的基础上连接OC.
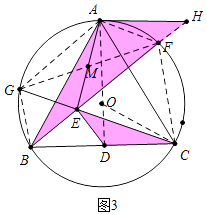
由(2)可知,△MFE≌△DCE,
∴∠FEM=∠CED,
∵AH=AE=4,
∴∠H=∠AEH,DE=2,
∴∠H=∠CED,
∵BG=GE=AF,
∴ ![]() =
= ![]() ,
,
∴∠ECD=∠ABH,
∴△AHB∽△DEC,
∴ ![]() =
= ![]() =2,设BE=x,EC=EF=y,BD=a,
=2,设BE=x,EC=EF=y,BD=a,
∴BH=2EC,
∴FH=y﹣x,
∵∠HAF=∠ABH,∠H=∠H,
∴△HAF∽△HBA,
∴AH2=HFHB,
∴16=2y(y﹣x) ①
∵BD=CD,∴AD⊥BC,AD经过点O,
∵AH是切线,
∴AH⊥AD,
∴AH∥BC,
∴∠H=∠CBE,
∴∠CED=∠CBE,∵∠ECD=∠ECB,
∴△ECD∽△BCE,
∴EC2=CDCB,
∴y2=a2a,
∴a= ![]() y,
y,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x=2 ![]() 代入①中解得y=
代入①中解得y= ![]() +
+ ![]() (负根已经舍弃),
(负根已经舍弃),
∴CD=a= ![]() (
( ![]() +
+ ![]() )=1+
)=1+ ![]() ,
,
在Rt△COD中,∵∠OCD=30°,
∴cos30°= ![]() ,
,
∴OC= ![]()
【解析】(1)利用“同圆中,等弦所对的劣弧相等”,得出∠GEB=∠FBC+∠ECB=∠ACE+∠ECB=60°,可求出∠BEC度数;(2)通过“连接BG、AG、CF、AF、GF,GF与AE交于点M“构造出四边形AGEF,利用等弧所对的圆周角相等,可证出四边形AGEF是平行四边形,进而证得△MFE≌△DCE,ME=DE,AE=2DE;(3)可证出△AHB∽△DEC,△HAF∽△HBA,得出AH2=HFHB,求出y与a 的关系,再由AH是切线,证出△ECD∽△BCE,对应边成比例,求出x,再利用30度角的余弦,得出OC与CD的关系,求出OC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
(2)如图(1),设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值.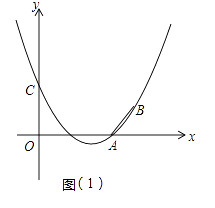
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用-5、-2、1,三个数按照给出顺序构造一组无限循环数据。
(1)求第2018个数是多少?
(2)求前50个数的和是多少?
(3)试用含![]() (
(![]() 为正整数)的式子表示出数“-2所在的位置数;
为正整数)的式子表示出数“-2所在的位置数;
(4)请你算出第![]() 个,第
个,第![]() 个,第
个,第![]() 个这三个数的和?
个这三个数的和?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“星光隧道”是贯穿新牌坊商圈和照母山以北的高端居住区的重要纽带,预计2017年底竣工通车,图中线段AB表示该工程的部分隧道,无人勘测飞机从隧道一侧的点A出发,沿着坡度为1:2的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为12°,继续飞行到点E,测得点B的俯角为45°,此时点E离地面高度EF=700米,则隧道BC段的长度约为( )米.(参考数据:tan12°≈0.2,cos12°≈0.98)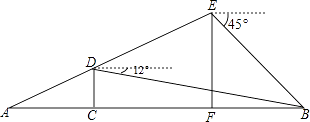
A.2100
B.1600
C.1500
D.1540
查看答案和解析>>
科目:初中数学 来源: 题型:
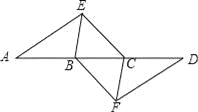
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com