
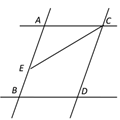
【题目】如图,已知AB∥CD,AC∥BD,CE平分∠ACD.
(1)求证:△ACE是等腰三角形;
(2)求证:∠BEC>∠BDC.
【答案】(1)证明见解析;(2)证明见解析
【解析】分析:(1)根据AB∥CD,得∠AEC=∠ECD,再根据角平分线的定义得出∠ACE=∠ECD,从而得出∠AEC=∠ECA,根据等角对等边,得出AC=AE;
(2)先判断ABDC为平行四边形,根据平行四边形的性质得出∠CAE=∠BDC,再根据外角的性质得出∠BEC>∠BDC.
本题解析:
(1)∵AB∥CD,
∴∠AEC=∠ECD,
∵CE平分∠ACD,
∴∠ACE=∠ECD,
∴∠AEC=∠ECA,
∴AC=AE,
∴△ACE是等腰三角形;
(2)∵AB∥CD,AC∥BD,
∴四边形ABDC为平行四边形,
∴∠CAE=∠BDC,
∵∠BEC>∠CAE,
∴∠BEC>∠BDC.


科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC为⊙O的内接三角形,点G和点F在⊙O上且位于点A的两侧,连接BF、CG交于点E,且BF=CG.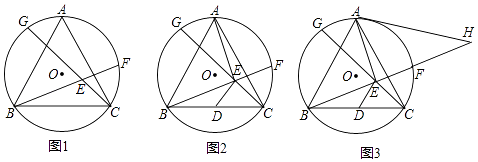
(1)求证:∠BEC=120°;
(2)如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;
(3)如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
, OA=10,E为x轴负半轴上一点,且tan∠AOE= ![]() .
.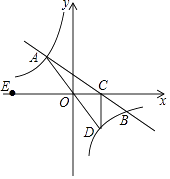
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)点 E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在甲乙两家超市发现他看中的一套运动服的单价相同,书包单价也相同.运动服和书包单价之和是452元,且运动服的单价比书包单价的4倍少8元.
(1)求该同学看中的运动服和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,甲超市所有商品打八折销售,乙超市全场每购满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,请说明他能在哪一家购买?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
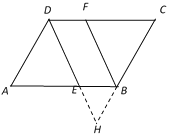
【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一蓄水池中有水40m3,如果每分钟放出2m3的水,水池里的水量与放水时间有如下关系:
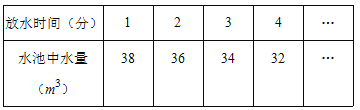
下列数据中满足此表格的是( )
A. 放水时间8分钟,水池中水量25m3
B. 放水时问20分钟,水池中水量4m3
C. 放水时间26分钟,水池中水量14m3
D. 放水时间18分钟,水池中水量4m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
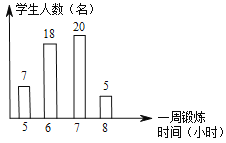
A. 中位数是6.5 B. 平均数高于众数
C. 极差为3 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com