
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 . 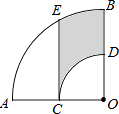
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“星光隧道”是贯穿新牌坊商圈和照母山以北的高端居住区的重要纽带,预计2017年底竣工通车,图中线段AB表示该工程的部分隧道,无人勘测飞机从隧道一侧的点A出发,沿着坡度为1:2的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为12°,继续飞行到点E,测得点B的俯角为45°,此时点E离地面高度EF=700米,则隧道BC段的长度约为( )米.(参考数据:tan12°≈0.2,cos12°≈0.98)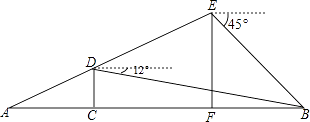
A.2100
B.1600
C.1500
D.1540
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )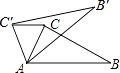
A.40°
B.50°
C.30°
D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2 ![]() ,AE=8,则S四边形EFMG= .
,AE=8,则S四边形EFMG= . 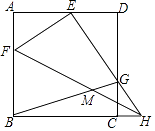
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD的对角线相交于O,点E,F分别在边AB、BC上,且BE=BF,射线EO,FO分别交边CD、AD于G,H.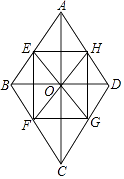
(1)求证:四边形EFGH为矩形;
(2)若OA=4,OB=3,求EG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
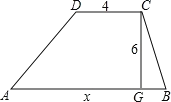
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com