
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2 ![]() ,AE=8,则S四边形EFMG= .
,AE=8,则S四边形EFMG= . 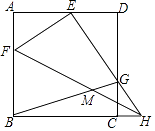
【答案】![]()
【解析】解:过B作BP⊥EH于P,连接BE,交FH于N,则∠BPG=90°,
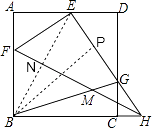
∵四边形ABCD是正方形,
∴∠BCD=∠ABC=∠BAD=90°,AB=BC,
∴∠BCD=∠BPG=90°,
∵∠EGB=∠CGB,BG=BG,
∴△BPG≌△BCG,
∴∠PBG=∠CBG,BP=BC,
∴AB=BP,
∵∠BAE=∠BPE=90°,BE=BE,
∴Rt△ABE≌Rt△PBE(HL),
∴∠ABE=∠PBE,
∴∠EBG=∠EBP+∠GBP= ![]() ∠ABC=45°,
∠ABC=45°,
由折叠得:BF=EF,BH=EH,
∴FH垂直平分BE,
∴△BNM是等腰直角三角形,
∵BM=2 ![]() ,
,
∴BN=NM= ![]() =2
=2 ![]() ,
,
∴BE=4 ![]() ,
,
∵AE=8,
∴DE=12﹣8=4,
由勾股定理得:AB= ![]() =
= ![]() =12,
=12,
设BF=x,则EF=x,AF=12﹣x,
由勾股定理得:x2=82+(12﹣x)2,
x= ![]() ,
,
∴BF=EF= ![]() ,
,
∵△ABE≌△PBE,
∴EP=AE=8,BP=AB=12,
同理可得:PG= ![]() ,
,
Rt△EFN中,FN= ![]() =
= ![]() ,
,
∴S四边形EFMG=S△EFN+S△EBG﹣S△BNM,
= ![]() FNEN+
FNEN+ ![]() ﹣
﹣ ![]() BNNM,
BNNM,
= ![]() ×
× ![]() ×
× ![]() +
+ ![]() (8+
(8+ ![]() )×12﹣
)×12﹣ ![]() ×
× ![]() ×
× ![]() ,
,
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.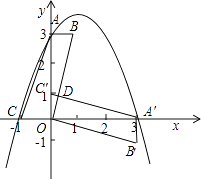
(1)若抛物线过点C,A,A',求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A'B'OC'重叠部分△OC'D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA'的面积最大?最大面积是多少?并求出此时M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)班学生参加毕业体考的成绩统计如图所示,请根据统计图中提供的信息完成后面的填空题(将答案填写在相应的横线上)
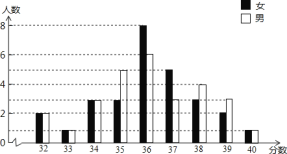
(1)该班共有______名学生;
(2)该班学生体考成绩的众数是______;男生体考成绩的中位数是______;
(3)若女生体考成绩在37分及其以上,男生体考成绩在38分及其以上被认定为体尖生,则该班共有_______名体尖生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 . 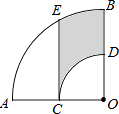
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A,B的坐标分别是(a,0),(b,0)且![]() .
.
(1)求点A,B的坐标;
(2)在y轴上是否存在点C,使△ABC的面积是15?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴负半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴方向以每秒2个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为18个平方单位?求此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
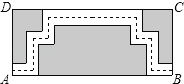
A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上M、O、N三点对应的数分别为﹣2、0、6,点P为数轴上任意一点,其对应的数为x.
![]()
(1)求MN的长;
(2)若点P是MN的中点,则x的值是 .
(3)数轴上是否存在一点P,使点P到点M、N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com