
【题目】已知数轴上M、O、N三点对应的数分别为﹣2、0、6,点P为数轴上任意一点,其对应的数为x.
![]()
(1)求MN的长;
(2)若点P是MN的中点,则x的值是 .
(3)数轴上是否存在一点P,使点P到点M、N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
【答案】(1)8;(2)2;(3)存在点P,x=﹣3或x=7,使PN+PM=10.
【解析】
(1)根据数轴上表示的数右边的总比左边的大的特点,利用N点与M点表示的数值差求MN长即可;
(2)先根据中点定义求出PN的长,再利用数轴上表示数的特点求出x的值;
(3)有两种情况:①点P在点M的左边,②点P在点N的右边,利用分类讨论的思想来解决问题.
解:(1)∵M、N对应的数分别为﹣2、6,
∴MN=6﹣(﹣2)=8;
(2)∵P是MN的中点,
∴![]()
∴x=2,故答案为2;
(3)存在点P到M、N的距离之和是10.
∵MN=8,
∴P点的位置可以分为两种情况:
①当点P在点M的左边时,PN+PM=10,
此时:(﹣2﹣x)+(6﹣x)=10,
解得:x=﹣3;
②当点P在点N的右边时,PN+PM=10,
此时:(x﹣6)+[x﹣(﹣2)]=10,
解得:x=7,
所以数轴上存在点P,x=﹣3或x=7,使PN+PM=10.


科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2 ![]() ,AE=8,则S四边形EFMG= .
,AE=8,则S四边形EFMG= . 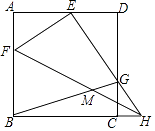
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣ ![]() (x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=
(x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y= ![]() x+
x+ ![]() 经过点A与对称轴交于E,点E的纵坐标为3.
经过点A与对称轴交于E,点E的纵坐标为3.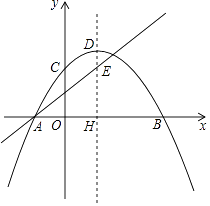
(1)求h、k的值;
(2)点P为第四象限抛物线上一点,连接PH,点Q为PH的中点,连接AQ、AP,设点P的横坐标为t,△AQP的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点Q作y轴的平行线QK,过点D作y轴的垂直DK,直线QK、DK交于点K,连接PK、EK,若2∠DKE+∠HPK=90°,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
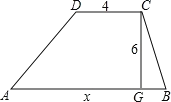
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
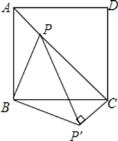
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 的坐标分
的坐标分![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒2个单位长度的速度沿着
从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动(即沿着长方形移动一周).
的路线移动(即沿着长方形移动一周).
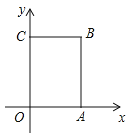
(1)写出点![]() 的坐标;
的坐标;
(2)当点![]() 移动了4秒时,求出点
移动了4秒时,求出点![]() 的坐标.
的坐标.
(3)在移动过程中,当点![]() 到
到![]() 轴的距离为5个单位长度时,求点
轴的距离为5个单位长度时,求点![]() 移动的时间.
移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com