
【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
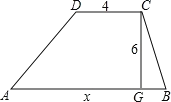
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
【答案】(1)y=![]() (4+x)×6=12﹣3x;(2)表格见解析;(3)由上表可得:x每增加1时,y减小3,理由见解析.
(4+x)×6=12﹣3x;(2)表格见解析;(3)由上表可得:x每增加1时,y减小3,理由见解析.
【解析】(1)利用梯形面积公式得出y与x 之间的关系;(2)结合关系式列表计算得出相关数据;(3)利用(1)中关系式,进而得出x每增加1时,y的变化.
解:(1)∵梯形ABCD上底的长是4,下底的长是x,高是6,
∴梯形ABCD的面积y与下底长x之间的关系式为:y=![]() (4+x)×6=12﹣3x;
(4+x)×6=12﹣3x;
(2)表格如下:
x | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
y | ﹣18 | ﹣21 | ﹣24 | ﹣27 | ﹣30 | ﹣33 | ﹣36 |
(3)由上表可得:x每增加1时,y减小3,
理由:y1=12﹣3x,y2=12﹣3(x+1)=12﹣3x﹣3=9﹣3x,
y2﹣y1=9﹣3x﹣(12﹣3x)=﹣3,即x每增加1时,y减小3.
“点睛”此题主要考查了函数关系式以及函数的变化,正确得出函数关系式是解题关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为 . 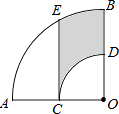
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在甲乙两家超市发现他看中的一套运动服的单价相同,书包单价也相同.运动服和书包单价之和是452元,且运动服的单价比书包单价的4倍少8元.
(1)求该同学看中的运动服和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,甲超市所有商品打八折销售,乙超市全场每购满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,请说明他能在哪一家购买?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
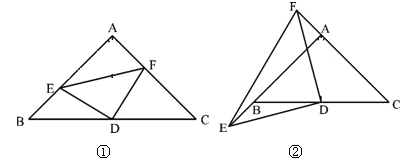
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一蓄水池中有水40m3,如果每分钟放出2m3的水,水池里的水量与放水时间有如下关系:
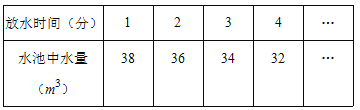
下列数据中满足此表格的是( )
A. 放水时间8分钟,水池中水量25m3
B. 放水时问20分钟,水池中水量4m3
C. 放水时间26分钟,水池中水量14m3
D. 放水时间18分钟,水池中水量4m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上M、O、N三点对应的数分别为﹣2、0、6,点P为数轴上任意一点,其对应的数为x.
![]()
(1)求MN的长;
(2)若点P是MN的中点,则x的值是 .
(3)数轴上是否存在一点P,使点P到点M、N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保持水土,美化环境,W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树,并要求土路两侧树的棵数相等间距也相等,且首、尾两端均栽上树,现在学校已备好一批树苗,若间隔30米栽一棵,则缺少22棵;若间隔35米栽一棵,则缺少14棵
(1)求学校备好的树苗棵数.
(2)某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后,觉得两树间距太大,既不美观,又影响防风固沙的效果,决定无偿支援W中学300棵树苗.请问,这些树苗加上学校自己备好的树苗,间隔5米栽一棵,是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).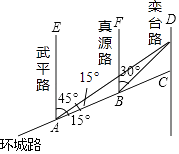
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,2016年10月1日起,聊城市公共自行车租赁系统(一期)试运行,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出)

请根据上面的统计图,解答下列问题:
(1)被调查的总人数是 ______ 人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com