
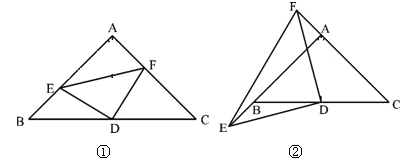
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)还是证明:△BED≌△AFD,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
试题解析:(1)连接AD,
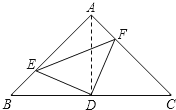
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)△DEF为等腰直角三角形.理由:
若E,F分别是AB,CA延长线上的点,如图所示:
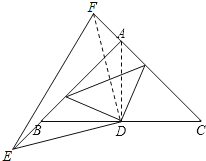
连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )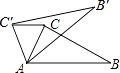
A.40°
B.50°
C.30°
D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣ ![]() (x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=
(x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y= ![]() x+
x+ ![]() 经过点A与对称轴交于E,点E的纵坐标为3.
经过点A与对称轴交于E,点E的纵坐标为3.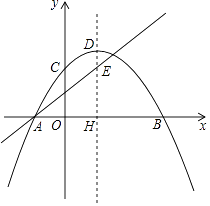
(1)求h、k的值;
(2)点P为第四象限抛物线上一点,连接PH,点Q为PH的中点,连接AQ、AP,设点P的横坐标为t,△AQP的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点Q作y轴的平行线QK,过点D作y轴的垂直DK,直线QK、DK交于点K,连接PK、EK,若2∠DKE+∠HPK=90°,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.
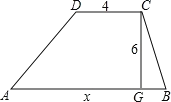
(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 的坐标分
的坐标分![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒2个单位长度的速度沿着
从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动(即沿着长方形移动一周).
的路线移动(即沿着长方形移动一周).
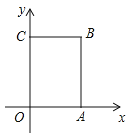
(1)写出点![]() 的坐标;
的坐标;
(2)当点![]() 移动了4秒时,求出点
移动了4秒时,求出点![]() 的坐标.
的坐标.
(3)在移动过程中,当点![]() 到
到![]() 轴的距离为5个单位长度时,求点
轴的距离为5个单位长度时,求点![]() 移动的时间.
移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让更多的居民享受免费的体育健身服务,重庆市将陆续建成多个社区健身点,某社区为了了解健身点的使用情况,现随机调查了部分社区居民,将调查结果分成四类,A:每天健身;B:经常健身;C:偶尔健身;D:从不健身;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图,解答下列问题: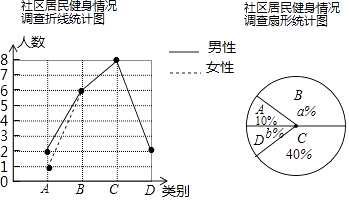
(1)本次调查中,一共调查了名社区居民,其中a=;请将折线统计图补充完整;
(2)为了吸引更多社区居民参加健身,健身点准备举办一次健身讲座培训,为此,想从被调查的A类和D类居民中分别选取一位在讲座上进行交流,请用列表法或画树状图的方法列出所有等可能的结果,并求出所选两位居民恰好是一位男性和一位女性的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com