
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпy=Љ ![]() ЃЈxЉhЃЉ2+kгыxжсНЛгкAЁЂBЃЌгыyжсНЛгкCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкHЃЌжБЯпy=
ЃЈxЉhЃЉ2+kгыxжсНЛгкAЁЂBЃЌгыyжсНЛгкCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкHЃЌжБЯпy= ![]() x+
x+ ![]() ОЙ§ЕуAгыЖдГЦжсНЛгкEЃЌЕуEЕФзнзјБъЮЊ3ЃЎ
ОЙ§ЕуAгыЖдГЦжсНЛгкEЃЌЕуEЕФзнзјБъЮЊ3ЃЎ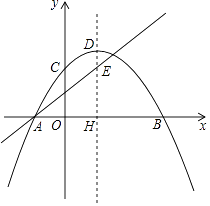
ЃЈ1ЃЉЧѓhЁЂkЕФжЕЃЛ
ЃЈ2ЃЉЕуPЮЊЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНгPHЃЌЕуQЮЊPHЕФжаЕуЃЌСЌНгAQЁЂAPЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЁїAQPЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЈжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуQзїyжсЕФЦНааЯпQKЃЌЙ§ЕуDзїyжсЕФДЙжБDKЃЌжБЯпQKЁЂDKНЛгкЕуKЃЌСЌНгPKЁЂEKЃЌШє2ЁЯDKE+ЁЯHPK=90ЁуЃЌЧѓЕуPЕФКсзјБъЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЁпЕуEЕФзнзјБъЮЊ3ЃЌ
Ёр3= ![]() x+
x+ ![]() ЃЌ
ЃЌ
НтЕУЃКx=2ЃЌ
ЁрDЕуЕФКсзјБъЪЧ2ЃЌ
Ёрh=2ЃЌ
ЁпжБЯпy= ![]() x+
x+ ![]() ОЙ§ЕуAЃЌ
ОЙ§ЕуAЃЌ
ЁрAЃЈЉ2ЃЌ0ЃЉДњШыy=Љ ![]() ЃЈxЉhЃЉ2+kЕУЃЌ0=Љ
ЃЈxЉhЃЉ2+kЕУЃЌ0=Љ ![]() ЃЈЉ2ЉhЃЉ2+kЃЌ
ЃЈЉ2ЉhЃЉ2+kЃЌ
Ёрk=4ЃЛ
ЃЈ2ЃЉНтЃКШчЭМ1ЃЌЩшPЕФКсзјБъЮЊtЃЌдђзнзјБъЮЊЉ ![]() t2+t+3ЃЌ
t2+t+3ЃЌ
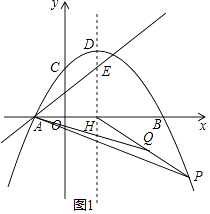
ЁпЕуQЮЊPHЕФжаЕуЃЌ
ЁрSЁїAPQ=SЁїAQHЃЌ
ЁрSЁїAPQ= ![]() SЁїAHPЃЌ
SЁїAHPЃЌ
ЁпSЁїAHP= ![]() AHЃЈ
AHЃЈ ![]() t2ЉtЉ3ЃЉЃЌ
t2ЉtЉ3ЃЉЃЌ
ЁпAH=4ЃЌ
ЁрS= ![]() ЁС4ЁСЃЈЃЈ
ЁС4ЁСЃЈЃЈ ![]() t2ЉtЉ3ЃЉ=
t2ЉtЉ3ЃЉ= ![]() t2ЉtЉ3ЃЈtЃО6ЃЉЃЛ
t2ЉtЉ3ЃЈtЃО6ЃЉЃЛ
ЃЈ3ЃЉНтЃКШчЭМ2ЃЌЙ§PзїxжсЁЂyжсЕФЦНааЯпЗжБ№НЛDHЃЌKQгкMЃЌNЃЌНЛжБЯпDKгкRЃЌ
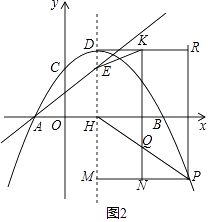
дђЫФБпаЮDKNMЃЌЫФБпаЮKNPRЪЧОиаЮЃЌ
ЩшMN=mЃЌ
ЁрDK=KR=mЃЌ
ЁрPЕуЕФКсзјБъЮЊ2m+2ЃЌДњШыy=Љ ![]() ЃЈxЉ2ЃЉ2+4жаЃЌ
ЃЈxЉ2ЃЉ2+4жаЃЌ
ЕУЕНPЕуЕФзнзјБъЮЊЃКЉm2+4ЃЌЁрDM=RP=m2ЃЌ
ЁрtanЁЯDKE= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрЁЯDKE=ЁЯKPRЃЌ
ЁрEKЁЭPKЃЌ
Ёп2ЁЯDKE+ЁЯHPK=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌ
ЁрЁЯDKE=ЁЯPHBЃЌ
ЁрtanЁЯDKE=tanЁЯPHBЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёрm=ЁР ![]() ЃЈm=Љ
ЃЈm=Љ ![]() ЩсШЅЃЉЃЌ
ЩсШЅЃЉЃЌ
Ёрm= ![]() ЃЌ
ЃЌ
ЁрЕуPЕФКсзјБъЮЊ2+2 ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЯШЧѓГіEЕФКсзјБъЃЌЕШгкDЕФКсзјБъЃЌМДhжЕЃЌдйАбAзјБъДњШыХзЮяЯпНтЮіЪНЧѓГіk;ЃЈ2ЃЉгЩЁАQЮЊPHЕФжаЕуЁБПЩжЊЁїAPQгыЁїAHPЪЧЭЌИпЕШЕзШ§НЧаЮЃЌУцЛ§ЯрЕШЃЌвђДЫПЩгУtЕФДњЪ§ЪНБэЪОSЁїAHPЃЌдйГЫвд![]() ;(3)гЩ"2ЁЯDKE+ЁЯHPK=90Ёу"ПЩЭЦГіЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌИљОнЖўепЕФе§ЧаЖЈвхЙЙНЈЕШЪНЃЌЧѓГіm.
;(3)гЩ"2ЁЯDKE+ЁЯHPK=90Ёу"ПЩЭЦГіЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌИљОнЖўепЕФе§ЧаЖЈвхЙЙНЈЕШЪНЃЌЧѓГіm.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХЃЈ1ЃЉАрбЇЩњВЮМгБЯвЕЬхПМЕФГЩМЈЭГМЦШчЭМЫљЪОЃЌЧыИљОнЭГМЦЭМжаЬсЙЉЕФаХЯЂЭъГЩКѓУцЕФЬюПеЬтЃЈНЋД№АИЬюаДдкЯргІЕФКсЯпЩЯЃЉ
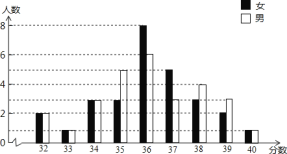
ЃЈ1ЃЉИУАрЙВга______УћбЇЩњЃЛ
ЃЈ2ЃЉИУАрбЇЩњЬхПМГЩМЈЕФжкЪ§ЪЧ______ЃЛФаЩњЬхПМГЩМЈЕФжаЮЛЪ§ЪЧ______ЃЛ
ЃЈ3ЃЉШєХЎЩњЬхПМГЩМЈдк37ЗжМАЦфвдЩЯЃЌФаЩњЬхПМГЩМЈдк38ЗжМАЦфвдЩЯБЛШЯЖЈЮЊЬхМтЩњЃЌдђИУАрЙВга_______УћЬхМтЩњЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђЯТСаИїЪН
ЃЈ1ЃЉЃЈb+2aЃЉЃЈ2aЉbЃЉЉ3ЃЈ2aЉbЃЉ2
ЃЈ2ЃЉ![]() ЁТЃЈ
ЁТЃЈ ![]() ЉaЉbЃЉ+
ЉaЉbЃЉ+ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГЙЋдАРявЛДІОиаЮЗчОАаРЩЭЧјABCDЃЌГЄAB=50УзЃЌПэBC=25УзЃЌЮЊЗНБугЮШЫЙлЩЭЃЌЙЋдАЬивтаоНЈСЫШчЭМЫљЪОЕФаЁТЗЃЈЭМжаЗЧвѕгАВПЗжЃЉЃЌаЁТЗЕФПэОљЮЊ1УзЃЌФЧаЁУїбизХаЁТЗЕФжаМфЃЌДгГіПкAЕНГіПкBЫљзпЕФТЗЯпЃЈЭМжаащЯпЃЉГЄЮЊЃЈ ЃЉ
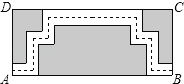
AЃЎ100Уз BЃЎ99Уз CЃЎ98Уз DЃЎ74Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭЌбЇдкМзввСНМвГЌЪаЗЂЯжЫћПДжаЕФвЛЬздЫЖЏЗўЕФЕЅМлЯрЭЌЃЌЪщАќЕЅМлвВЯрЭЌЃЎдЫЖЏЗўКЭЪщАќЕЅМлжЎКЭЪЧ452дЊЃЌЧвдЫЖЏЗўЕФЕЅМлБШЪщАќЕЅМлЕФ4БЖЩй8дЊЃЎ
ЃЈ1ЃЉЧѓИУЭЌбЇПДжаЕФдЫЖЏЗўКЭЪщАќЕФЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉФГвЛЬьИУЭЌбЇЩЯНжЃЌЧЁКУИЯЩЯЩЬМвДйЯњЃЌМзГЌЪаЫљгаЩЬЦЗДђАЫелЯњЪлЃЌввГЌЪаШЋГЁУПЙКТњ100дЊЗЕЙКЮяШЏ30дЊЯњЪл(ВЛзу100дЊВЛЗЕШЏЃЌЙКЮяШЏШЋГЁЭЈгУ)ЃЌЕЋЫћжЛДјСЫ400дЊЧЎЃЌШчЙћЫћжЛдквЛМвГЌЪаЙКТђПДжаЕФетСНбљЮяЦЗЃЌЧыЫЕУїЫћФмдкФФвЛМвЙКТђЃПШєСНМвЖМПЩвдбЁдёЃЌдкФФвЛМвЙКТђИќЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЁбOНЛBCЕФжаЕугкDЃЌDEЁЭACгкЕуEЃЌСЌНгADЃЌдђЯТСаНсТле§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЂйADЁЭBCЃЛЂкЁЯEDA=ЁЯBЃЛЂлOA= ![]() ACЃЛЂмDEЪЧЁбOЕФЧаЯпЃЎ
ACЃЛЂмDEЪЧЁбOЕФЧаЯпЃЎ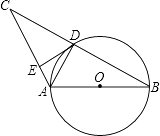
A.1Иі
B.2Иі
C.3Иі
D.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШ§НЧаЮABCжаЃЌЁЯAЃН90ЁуЃЌABЃНACЃЌDЮЊBCЕФжаЕуЃЌ
ЃЈ1ЃЉШчЭМЂйЃЌEЃЌFЗжБ№ЪЧABЃЌACЩЯЕФЕуЃЌЧвBEЃНAFЃЌЧѓжЄЃКЁїDEFЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌШєEЃЌFЗжБ№ЮЊABЃЌCAбгГЄЯпЩЯЕФЕуЃЌШдгаBEЃНAFЃЌЦфЫћЬѕМўВЛБфЃЌФЧУДЁїDEFЪЧЗёШдЮЊЕШбќжБНЧШ§НЧаЮЃПжЄУїФуЕФНсТлЃЎ
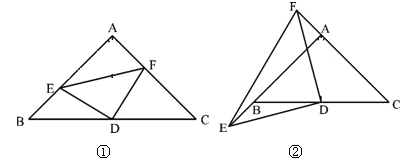
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯMЁЂOЁЂNШ§ЕуЖдгІЕФЪ§ЗжБ№ЮЊЉ2ЁЂ0ЁЂ6ЃЌЕуPЮЊЪ§жсЩЯШЮвтвЛЕуЃЌЦфЖдгІЕФЪ§ЮЊxЃЎ
![]()
ЃЈ1ЃЉЧѓMNЕФГЄЃЛ
ЃЈ2ЃЉШєЕуPЪЧMNЕФжаЕуЃЌдђxЕФжЕЪЧЁЁ ЁЁЃЎ
ЃЈ3ЃЉЪ§жсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕуPЕНЕуMЁЂNЕФОрРыжЎКЭЪЧ10ЃПШєДцдкЃЌЧѓГіxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђЃЌдйЧѓжЕЃК
(1)2aЃЋ3(a2Ѓb)Ѓ2(2a2ЃЋaЃ![]() b)ЃЌЦфжаaЃН
b)ЃЌЦфжаaЃН![]() ЃЌbЃНЃ2ЃЛ
ЃЌbЃНЃ2ЃЛ
(2)(mЃ5nЃЋ4mn)Ѓ2(2mЃ4nЃЋ6mn)ЃЌЦфжаmЃnЃН4ЃЌmnЃНЃ3.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com