[题目]先化简.再求值:(1)2a+3(a2-b)-2(2a2+a-b).其中a＝.b＝-2,(2)(m-5n+4mn)-2(2m-4n+6mn).其中m-n＝4.mn＝-3. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】先化简，再求值：

(1)2a＋3(a2－b)－2(2a2＋a－b)，其中a＝，b＝－2；

(2)(m－5n＋4mn)－2(2m－4n＋6mn)，其中m－n＝4，mn＝－3.

【答案】（1）－a2-2b，；（2）-3m+3n-8mn，12.

【解析】

（1）根据去括号法则及合并同类项法则把所给的整式化为最简后再代入求值即可；（2）根据去括号法则及合并同类项法则把所给的整式化为最简后再整体代入求值即可.

(1)2a＋3(a2－b)－2(2a2＋a－b)，

=2a＋3a2－3b－4a2-2a+b

=－a2-2b

当a＝，b＝－2时，

原式==.

（2）(m－5n＋4mn)－2(2m－4n＋6mn)

=m－5n＋4mn－4m+8n-12mn

=-3m+3n-8mn

=-3（m-n）-8mn

当m－n＝4，mn＝－3时，

原式=-3×4-8×（-3）=-12+24=12.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知：如图，抛物线y=﹣ （x﹣h）2+k与x轴交于A、B，与y轴交于C，抛物线的顶点为D，对称轴交x轴于H，直线y= x+ 经过点A与对称轴交于E，点E的纵坐标为3．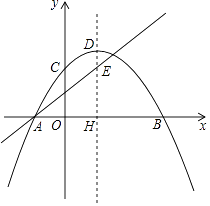

（1）求h、k的值；
（2）点P为第四象限抛物线上一点，连接PH，点Q为PH的中点，连接AQ、AP，设点P的横坐标为t，△AQP的面积为S，求S与t的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，过点Q作y轴的平行线QK，过点D作y轴的垂直DK，直线QK、DK交于点K，连接PK、EK，若2∠DKE+∠HPK=90°，求点P的横坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

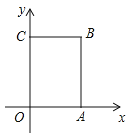
【题目】如图，在长方形中，为平面直角坐标系的原点，点的坐标分，点的坐标为，点在第一象限内，点从原点出发，以每秒2个单位长度的速度沿着的路线移动（即沿着长方形移动一周）．

（1）写出点的坐标；

（2）当点移动了4秒时，求出点的坐标．

（3）在移动过程中，当点到轴的距离为5个单位长度时，求点移动的时间．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线AB、CD相交于点O，OE把∠BOD分成两部分；

（1）直接写出图中∠AOC的对顶角为　　，∠BOE的邻补角为　　；

（2）若∠AOC＝70°，且∠BOE：∠EOD＝2：3，求∠AOE的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】襄江中学组织九年级部分学生到古隆中参观，租用的客车有50座和30座两种可供选择．学校根据参加参观的学生人数计算可知：若只租用30座客车x辆，还差10人才能坐满；若只租用50座客车，比只租用30座客车少用2辆，且有一辆车没有坐满但超过30人．
（1）写出九年级参观的学生人数y与x的关系式；
（2）求出此次参观的九年级学生人数；
（3）若租用一辆30座客车往返费用为260元，租用一辆50座客车往返费用为400元，如何选择租车方案费用最低？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，∠BAC=90°，AB=AC，D是BC上的点．求证：BD2+CD2=2AD2．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了让更多的居民享受免费的体育健身服务，重庆市将陆续建成多个社区健身点，某社区为了了解健身点的使用情况，现随机调查了部分社区居民，将调查结果分成四类，A：每天健身；B：经常健身；C：偶尔健身；D：从不健身；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图，解答下列问题：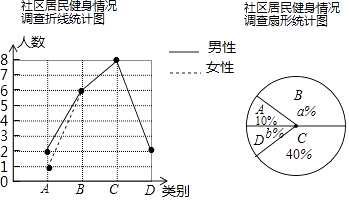

（1）本次调查中，一共调查了名社区居民，其中a=；请将折线统计图补充完整；
（2）为了吸引更多社区居民参加健身，健身点准备举办一次健身讲座培训，为此，想从被调查的A类和D类居民中分别选取一位在讲座上进行交流，请用列表法或画树状图的方法列出所有等可能的结果，并求出所选两位居民恰好是一位男性和一位女性的概率．