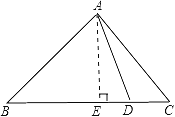
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，D是BC上的点．求证：BD2+CD2=2AD2．

参考答案：

【答案】证明过程见解析

【解析】

试题分析：作AE⊥BC于E，由于∠BAC=90°，AB=AC，所以BE=CE，要证明BD2+CD2=2AD2，只需找出BD、CD、AD三者之间的关系即可，由勾股定理可得出AD2=AE2+ED2，AE2=AB2﹣BE2=AC2﹣CE2，ED=BD﹣BE=CE﹣CD，代入求出三者之间的关系即可得证．

试题解析：作AE⊥BC于E，如上图所示： 由题意得：ED=BD﹣BE=CE﹣CD，

∵在△ABC中，∠BAC=90°，AB=AC， ∴BE=CE=BC， 由勾股定理可得：

AB2+AC2=BC2， AE2=AB2﹣BE2=AC2﹣CE2， AD2=AE2+ED2，

∴2AD2=2AE2+2ED2=AB2﹣BE2+（BD﹣BE）2+AC2﹣CE2+（CE﹣CD）2

=AB2+AC2+BD2+CD2﹣2BD×BE﹣2CD×CE =AB2+AC2+BD2+CD2﹣2×BC×BC

=BD2+CD2， 即：BD2+CD2=2AD2．

关闭